§ 16. Параллельность прямых и плоскостей → номер 25
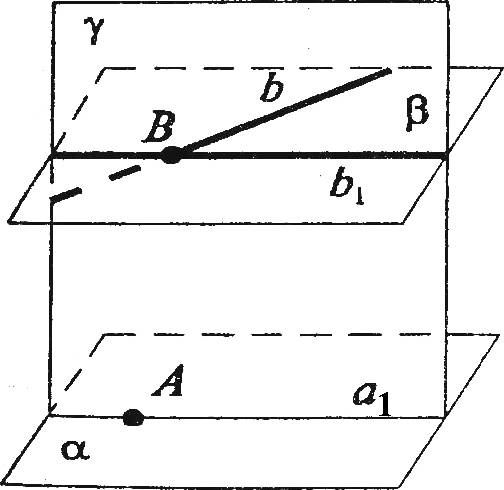
Пусть B — данная точка и α — данная плоскость. Проведем через точку В плоскость β, параллельную плоскости α.
Пусть b произвольная прямая, проходящая через точку B, параллельно α. Возьмем в плоскости α произвольную точку А и проведем через точку А и прямую b плоскость γ Тогда плоскость γ пересекает плоскости α и β по параллельным прямым а1 и b1, но прямая b1 проходит через точку В, а прямая b тоже лежит в плоскости γ, и проходит через точку В и по теореме 17.3 (обратной) параллельна прямой а1. Тогда по аксиоме прямые b и b1 должны совпадать, поэтому прямая b лежит в плоскости в, что и требовалось доказать.
