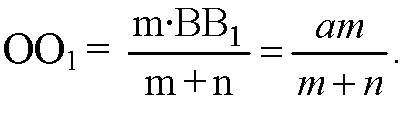§17. Перпендикулярность прямых и плоскостей → номер 39
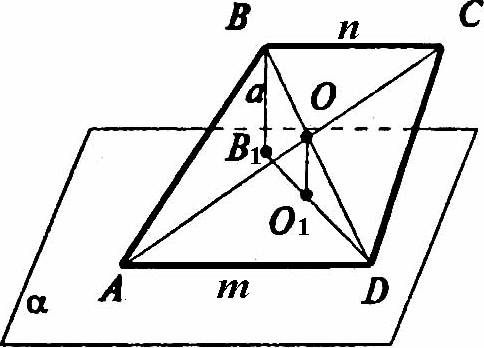
Пусть ABCD и α — данные трапеция и плоскость. О — точка пересечения диагоналей трапеции. ВВ1 и ОО1 — перпендикуляры к плоскости α. Тогда BB1 = a. Так как ΔOAD ~ ΔOCB, то
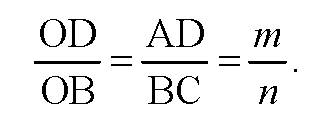
Далее рассмотрим ΔBB1D ВВ1 и ОО1 лежат в плоскости ВВ1D. DO1O~ВВ1D так как ∠B1DB — общий и ∠OO1D = ∠BB1D = 90°.
Тогда
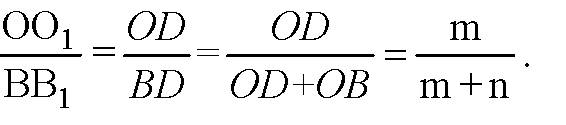
Так что