§17. Перпендикулярность прямых и плоскостей → номер 55
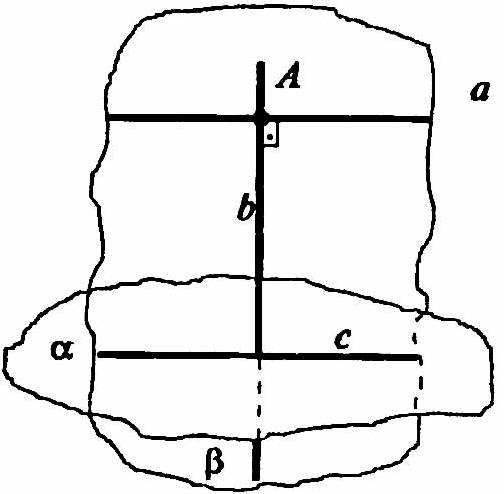
Возьмем любую точку А на прямой а, и проведем через нее прямую b ⊥ а. Плоскость β, образованная прямыми а и b, пересекает α по прямой с и b ⊥ с. Плоскости α и β перпендикулярны. Так как b ⊥ α и β содержит b. Любая прямая перпендикулярная а — должна быть параллельна b. А так как она пересекает а, то лежит в β. Что и требовалось доказать.
