Дополнительные задачи к главе I Параллельность прямых и плоскостей. → номер 109
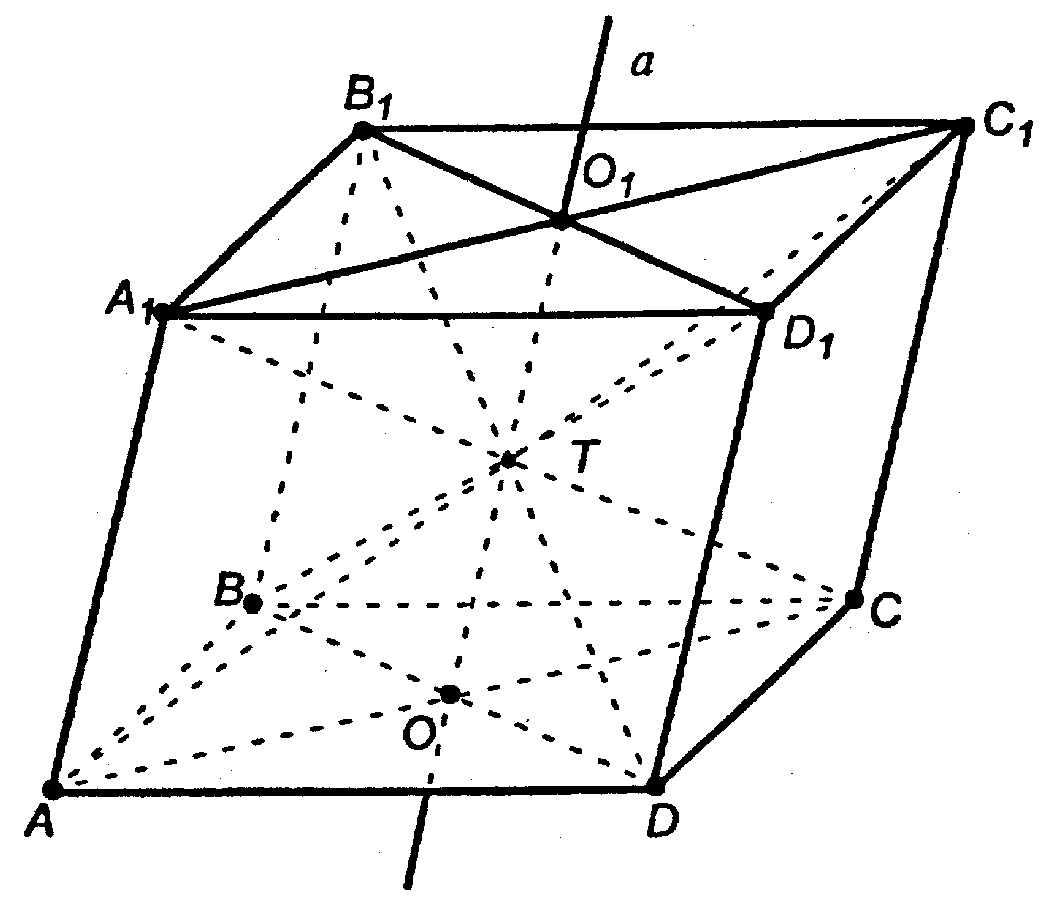
Доказательство
1. По условию, искомая прямая а есть линия пересечения двух плоскостей: АА1С1С и ВВ1D1D.
2. Проведем диагонали оснований параллелепипеда; они пересекаются в т. О1 и т. О.
3.
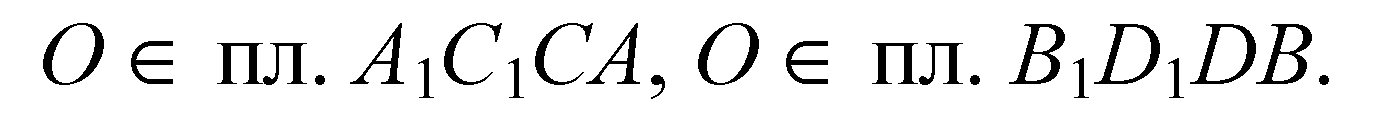
Т. О1 принадлежит тем же плоскостям. Следовательно, ОО1 — прямая пересечения этих плоскостей (аксиома А2).
4. Прямая а есть прямая ОО1.
5. Основания параллелепипеда — равные параллелограммы; по свойству параллелограмма А1О1=О1С1 = =АО = ОС.
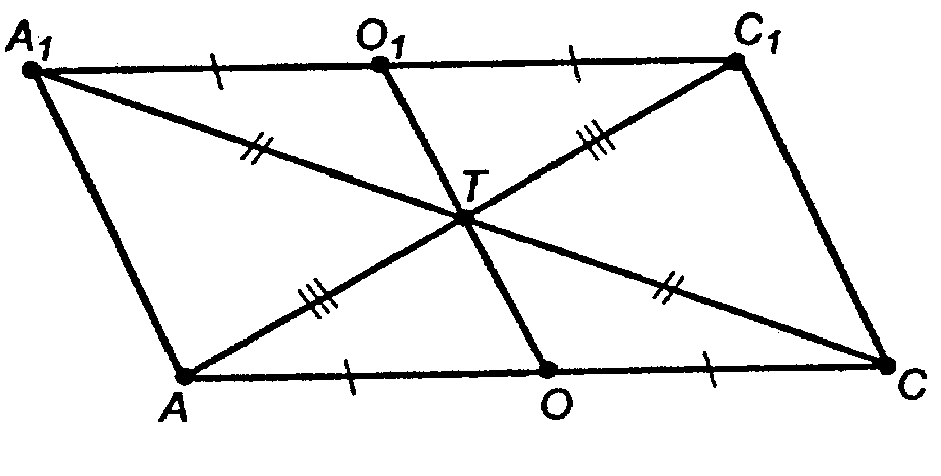
6. А1О1ОА — параллелограмм, значит,
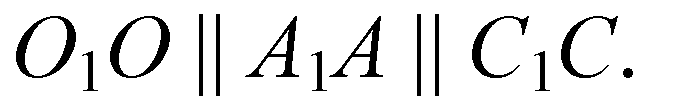
7. Аналогично получаем, что
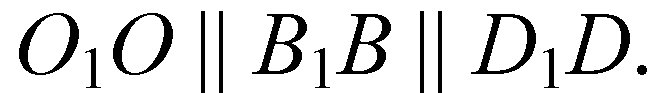
8. Проведем диагонали АС1 и А1С. Раз А1С1СА — параллелограмм, то А1Т = ТС, АТ = ТС 1, где Т — точка пересечения диагоналей.
9. ОТ — средняя линия АА1СА; О1Т — средняя линия ΔА1СС1.
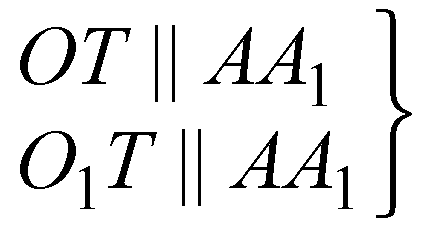
По аксиоме о параллельных прямых в плоскости точ
Ки О, О1 и Т лежат на одной прямой, Т ∈ ОО1, или Т ∈ а. Диагонали параллелепипеда и прямая а пересекаются в одной точке.
