139. Из некоторой точки проведены к плоскости две наклонные. Докажите, что: а) если наклонные равны, то равны и их проекции; б) если проекции наклонных равны, то равны и наклонные; в) если наклонные не равны, то большая наклонная имеет большую проекцию

Глава II Перпендикулярность прямых и плоскостей. §2 Перпендикуляр и наклонные. Угол между прямой и плоскостью. → номер 139 139. Из некоторой точки проведены к плоскости две наклонные. Докажите, что: а) если наклонные равны, то равны и их проекции; б) если проекции наклонных равны, то равны и наклонные; в) если наклонные не равны, то большая наклонная имеет большую проекцию.

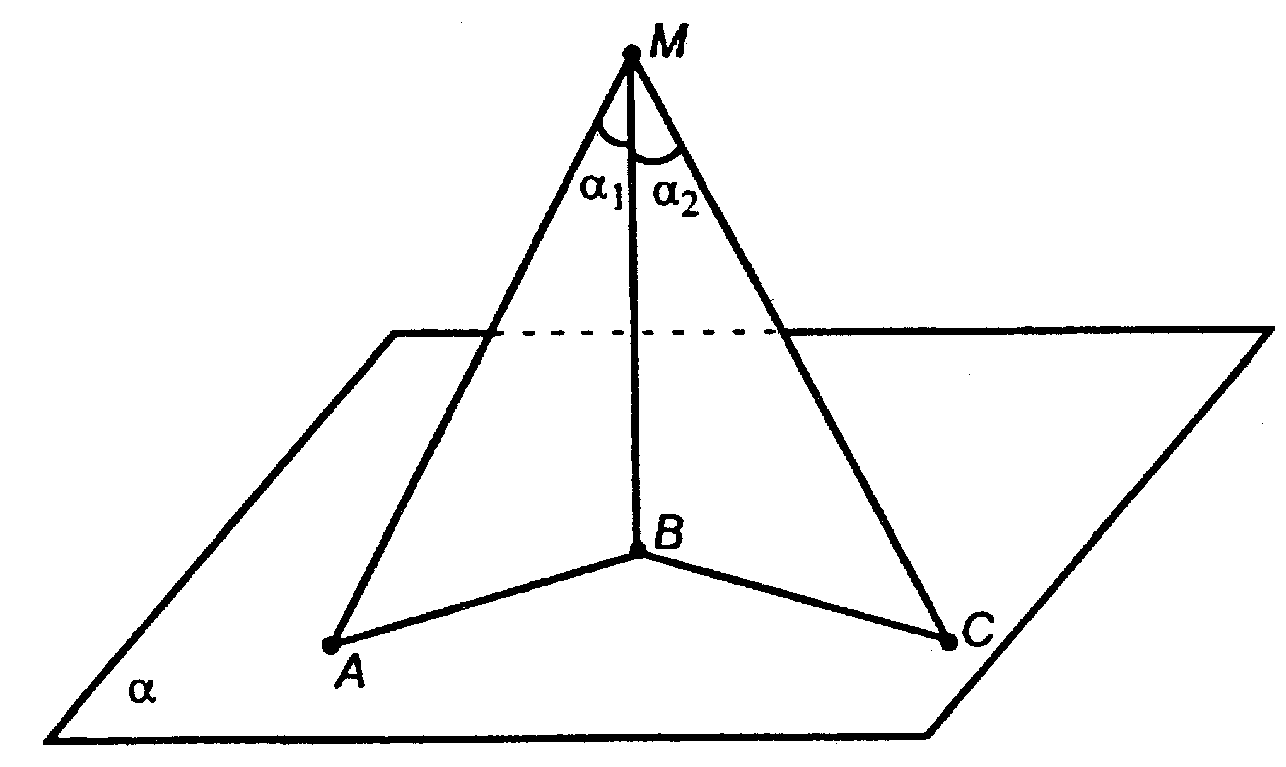
Решение:

А) МА = МС (по условию);

ΔМВА и ΔМВС — прямоугольные, МВ — общий катет, МА = МС, следовательно, ΔМВА = ΔМВС, значит, АВ = ВС.

Б) ВА = ВС (по условию).

Из равенства прямоугольных треугольников МВА и МВС следует, что МА = МС.

В) МА > MC (по условию).

По теореме Пифагора

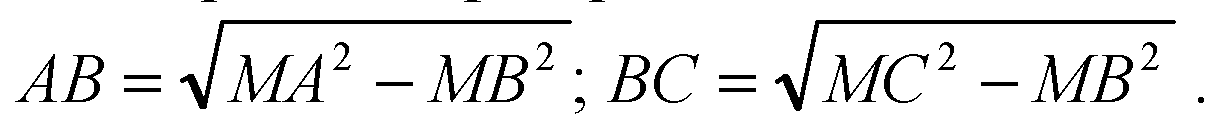
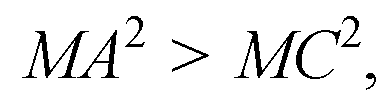
Поэтому

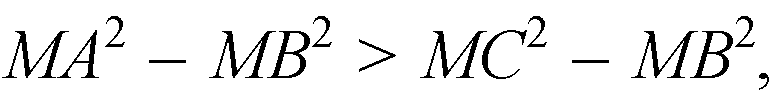
Это означает, что

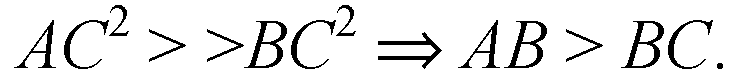
Что и требовалось доказать.