Глава II Перпендикулярность прямых и плоскостей. §2 Перпендикуляр и наклонные. Угол между прямой и плоскостью. → номер 161
Дано:
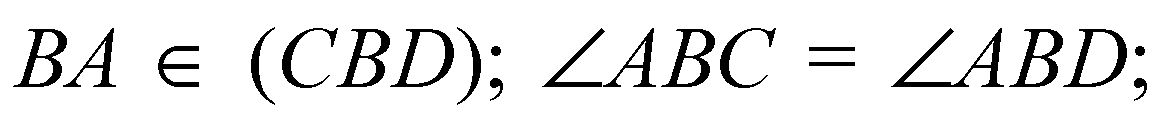
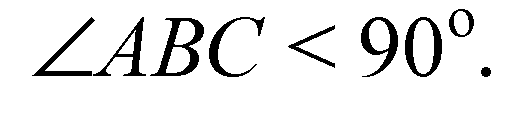
Решение:
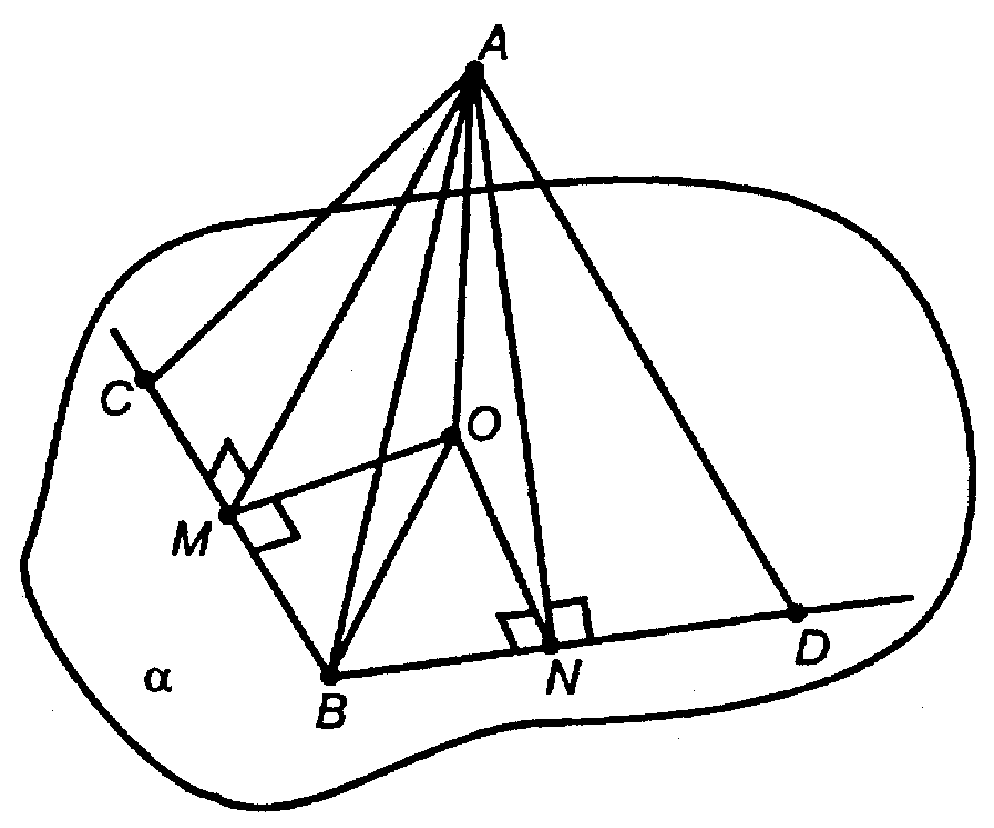
Проведем АО ⊥ α.
В пл. α проведем ОМ⊥СВ и ON⊥BD. По теореме о 3-х перпендикулярах
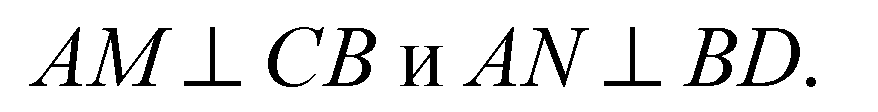
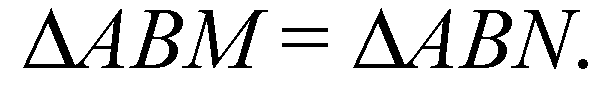
Поэтому
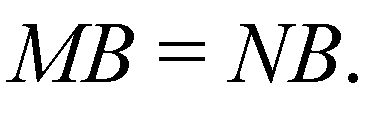
Проведем в пл. α отрезок ОВ. Рассмотрим ΔОВМ и ΔOBN.
У них сторона ОВ — общая, ВМ = BN (см. выше), оба треугольника — прямоугольные. Следовательно, ΔОВМ = ΔOBN, ∠ОВМ = ∠OBN и проекция ОВ наклонной ВА является биссектрисой ∠CBD.
Что и требовалось доказать.
