Дополнительные задачи к главе II Перпендикулярность прямых и плоскостей. → номер 200
Решение:
Пусть SO L а — данная прямая, а а — плоскость многоугольника
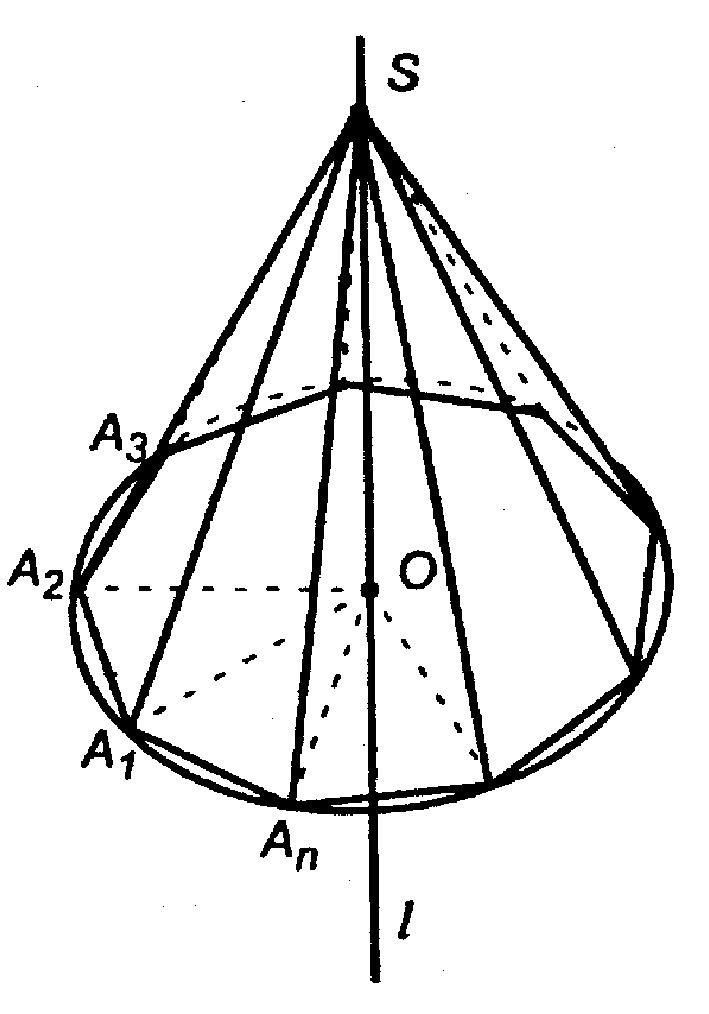
Пусть на плоскости а имеется вписанный в окружность n-угольник (не обязательно правильный n-угольник); т. О — центр описанной окружности.
Рассмотрим ΔA1OS, ΔA2OS, …, ΔAnOS. Они — прямоугольные, ОА1 = ОА2 = … = =ОАn — как радиусы окружности, SO — общий катет. Все треугольники равны, поэтому наклонные SA1, SA2, …, SАn тоже равны. Это суть утверждение задачи.
