Глава III Многогранники. § 2. Пирамида → номер 249
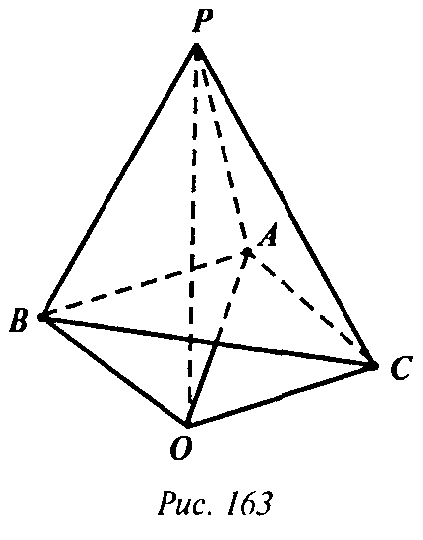
а) Рассмотрим пирамиду РА1А3… Аn и пусть высота пирамиды РО. Заметим, что ΔPOA1 = ΔРОА2 по признаку равенства прямоугольных треугольников (по двум сторонам).
Значит
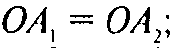
Аналогично
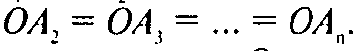
Но это и означает, что точка О — центр описанной окружности. б) Так как ОА1 — проекция стороны РА1, то угол РА1O и есть угол между ребром РА1 и основанием. Но из равенства треугольников:
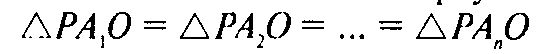
Следует равенство углов между боковыми ребрами и плоскостью основания.
