263. В правильной пирамиде MABCD точки К, L и N лежат на ребрах ВС, МС и AD, KN||BA, KL||BM. а) Покройте сечение пирамиды плоскостью KLN и определите вид сечения. б) Докажите, что плоскость KLN параллельна плоскости АМВ

Глава III Многогранники. § 2. Пирамида → номер 263

а) Прямая CD || KN поэтому линия пересечения плоскости сечения и плоскости MCD параллельна CD. Поэтому проведем LP||CD, где точка Р лежит на прямой МD. Соединим Р с N. KLPN — искомое сечение. Так как KN || СD, PL || CD, то KN || PL, и так как KN = CD, a PL ≠ CD, to KN ≠ PL, поэтому искомое сечение — трапеция.

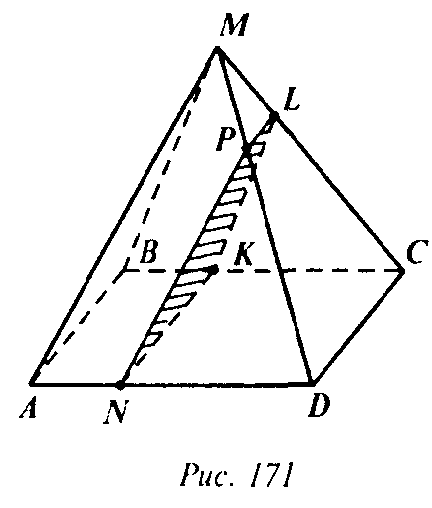
Б) По условию NK || AB, KL || ВМ, следовательно по теореме п.10 следует, что плоскости АМВ и KLN параллельны.