372. Докажите, что диагональ АС1 параллелепипеда ABCDA1B1C1D1 проходит через точки пересечения медиан треугольников A1BD и CB1D1 и делится этими точками на три равных отрезка (рис. 111)

Глава IV. Векторы в пространстве § 3. Компланарные вектора → номер 372 372. Докажите, что диагональ АС1 параллелепипеда ABCDA1B1C1D1 проходит через точки пересечения медиан треугольников A1BD и CB1D1 и делится этими точками на три равных отрезка (рис. 111).

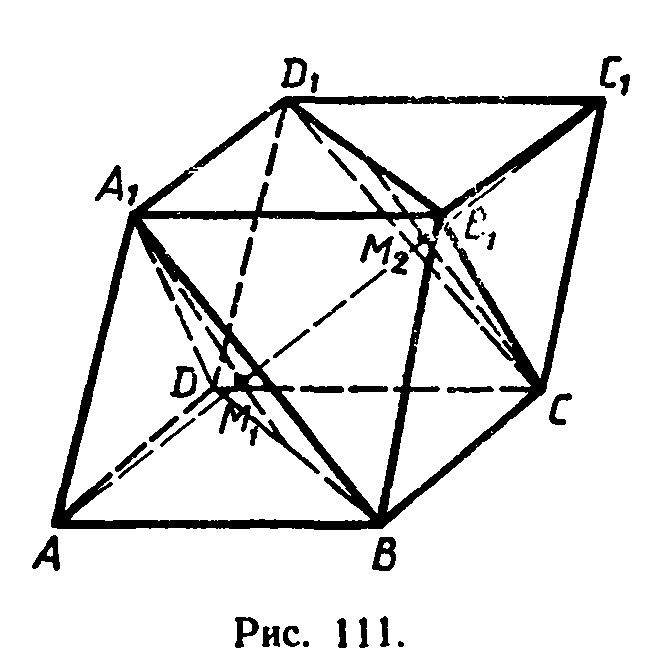
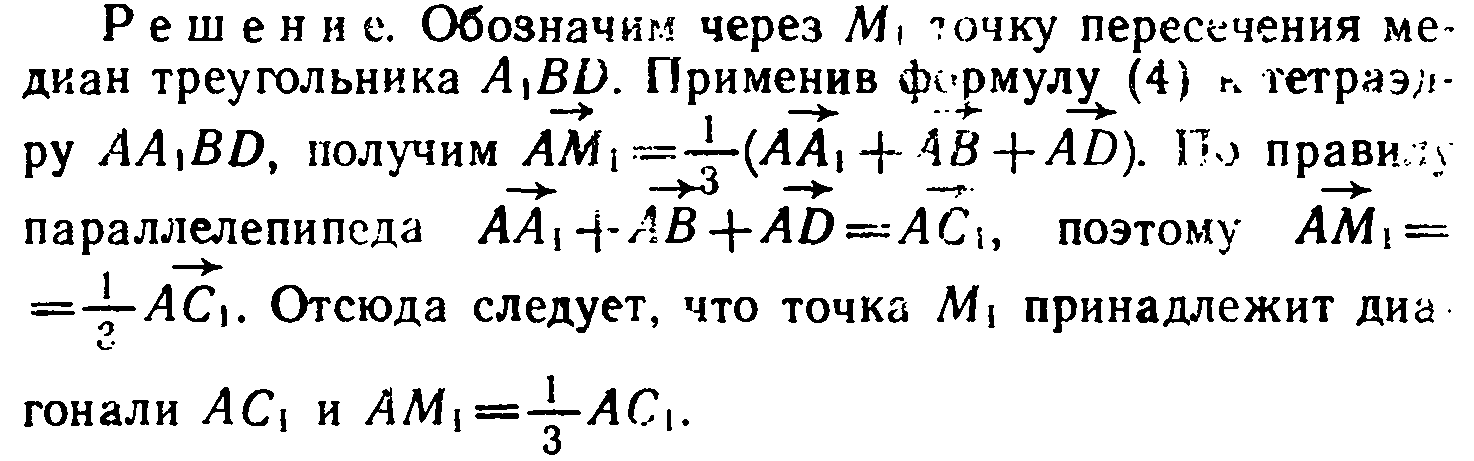
Точно так же можно доказать, что точка M2 пересечения медиан треугольника CB1D1 принадлежит диагонали АС1 и

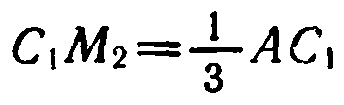
Из равенств

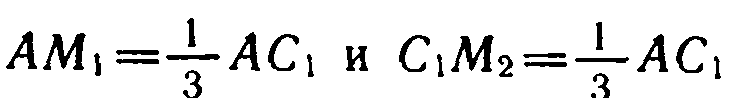
Следует, что точки М1 и М2 делят диагональ AC1 параллелепипеда на три равных отрезка AM1, M1M2 и M2C1.