423. Докажите, что точка пересечения медиан треугольника ABC с вершинами A (x1; y1; z1), В (x2; y2; z2), С (x3; y3; z3) имеет координаты

Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора. → номер 423

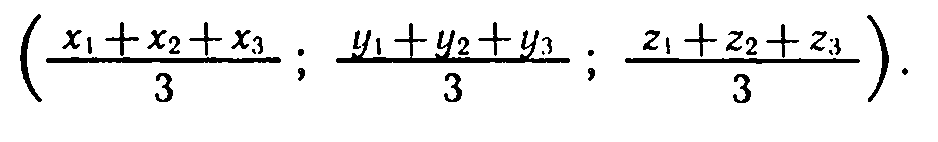Пусть AA1, ВВ1 и CC1 — медианы треугольника ABC, а M — точка их пересечения. Докажем, что точка M имеет координаты

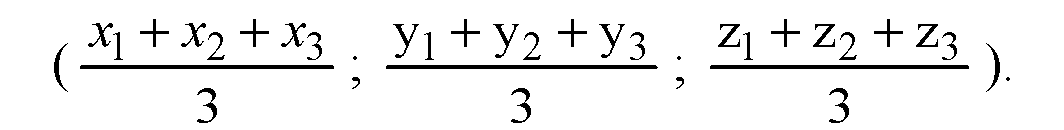
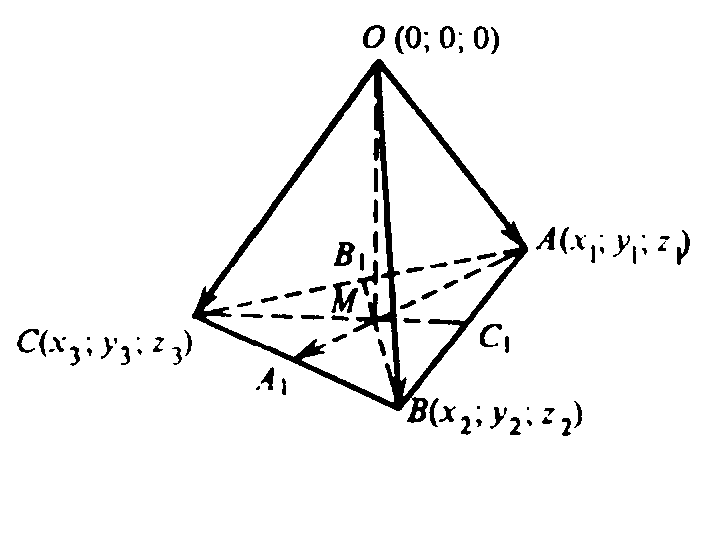
Координаты точки равны координатам ее радиус-вектора. Выберем произвольно начало координат и начертим радиус-векторы

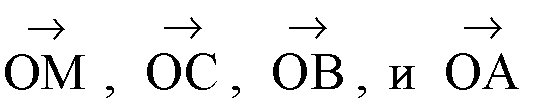
Их координаты будут соответствовать координатам точек M, С, В, А соответственно. По теореме о точке пересечения медиан треугольника

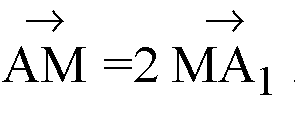
Так как

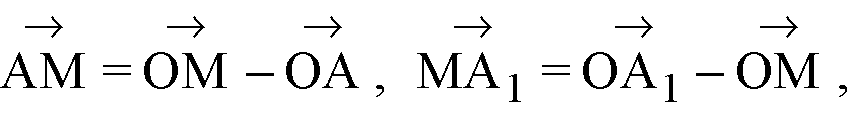
То, подставив эти разности

В наше равенство, получим:

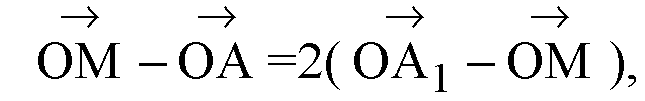
Или

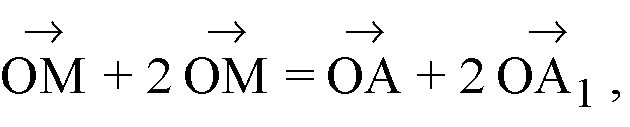
Или

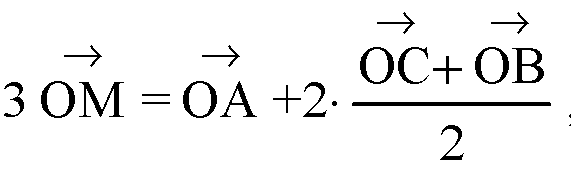
Т. к.

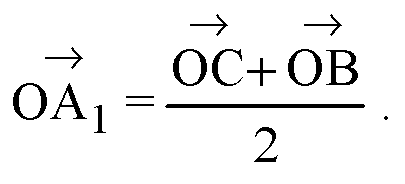
Следовательно,

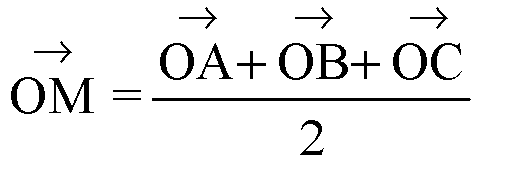
Или,

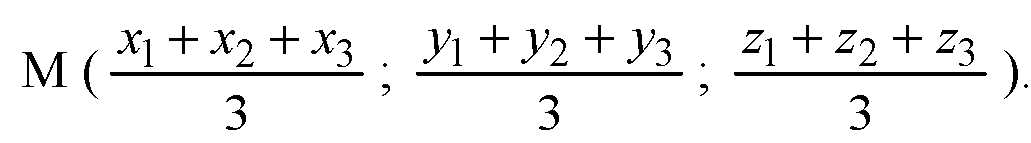
Доказано.