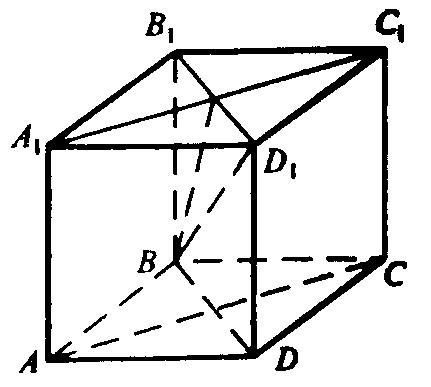
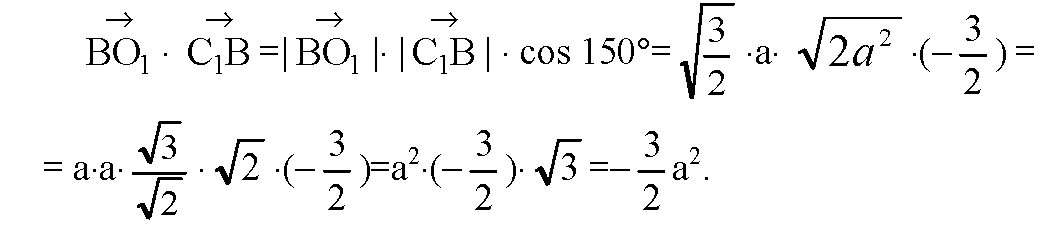Глава V. Метод координат в пространстве. § 2. Скалярное произведение векторов → номер 443 443. Ребро куба ABCDA1B1C1D1 равно а, точка O1 — центр грани A1B1C1D1. Вычислите скалярное произведение векторов: а) AD и В1С1; б) АС и С1А1; в) D1B и АС; г) ВА1 и ВС1; д) A1O1 и А1С1; е) D1O1 и В1O1; ж) ВО1 и С1В.
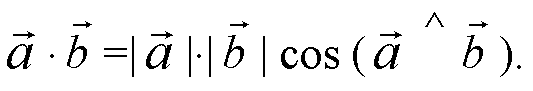
A)
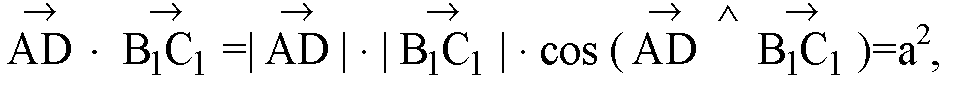
Т. к.
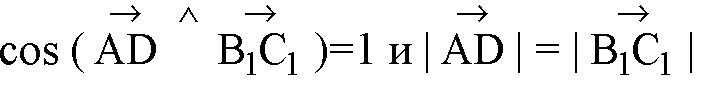
Б)
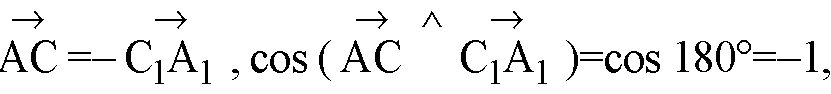
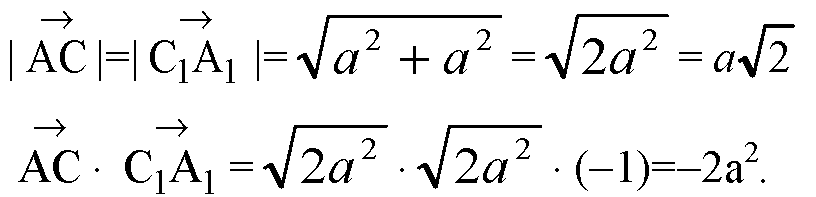
В)
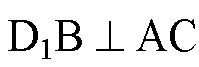
(по теореме о трех перпендикулярах),
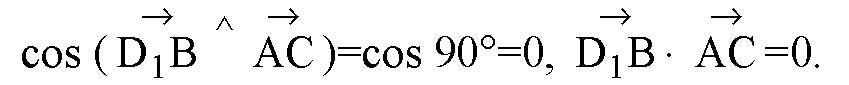
Г)
BA1 совпадает с диагональю грани куба, как и BC1
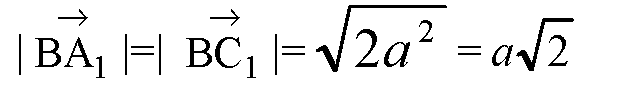
— равносторонний,
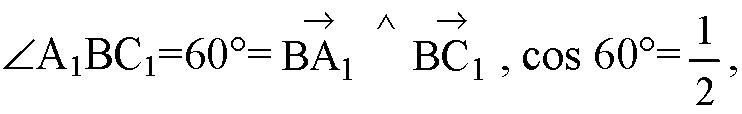
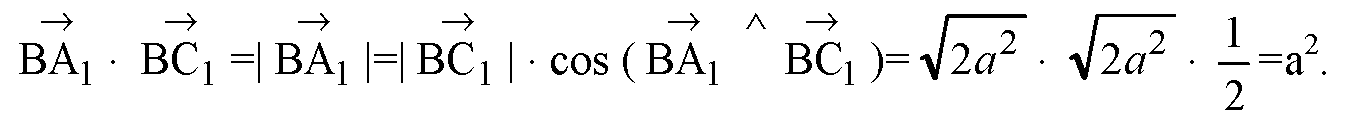
Д)
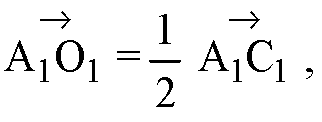
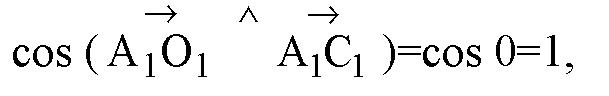
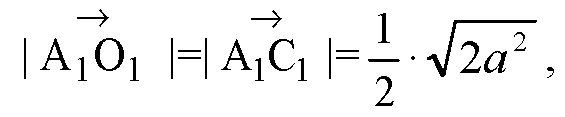
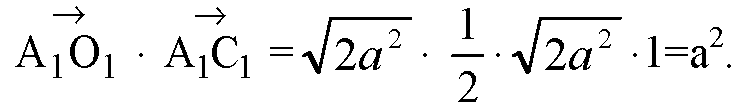
Е)
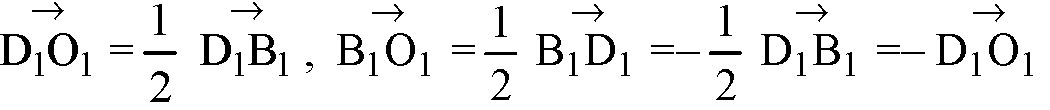
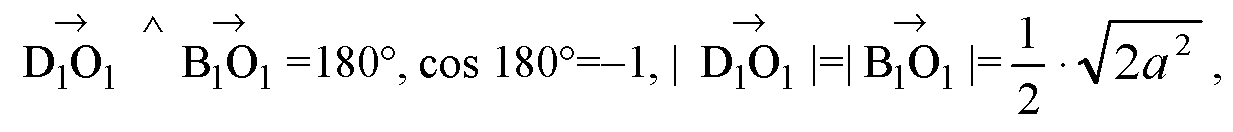
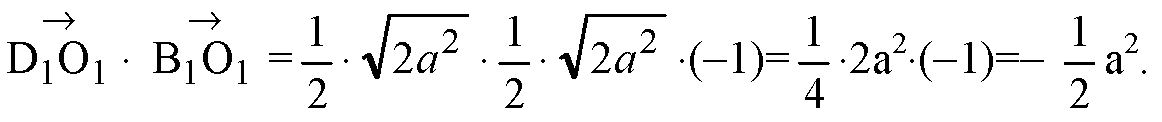
—
Ж) BO1 совпадает с гипотенузой прямоугольного ΔBB1O1, у которого катеты:
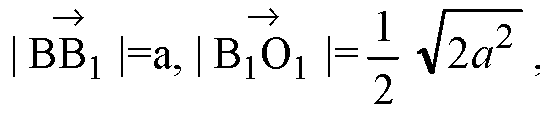
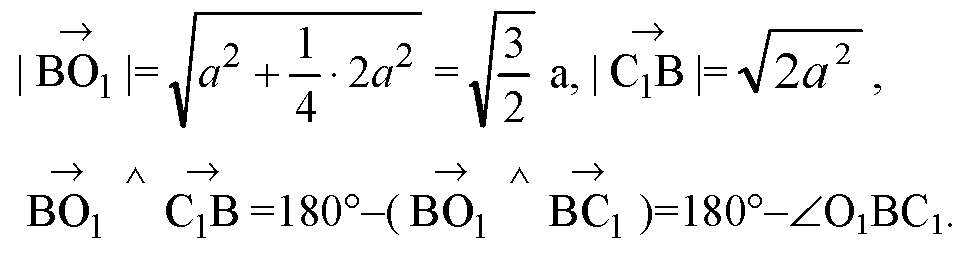
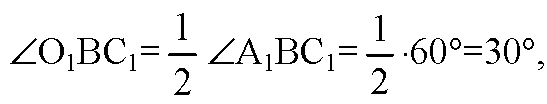
Т. к. ΔBA1C1 — равносторонний