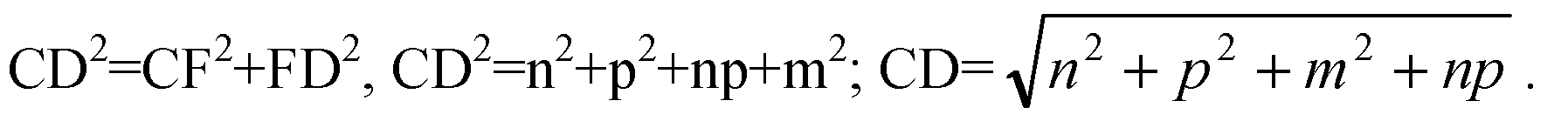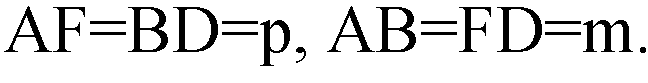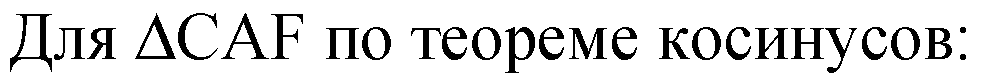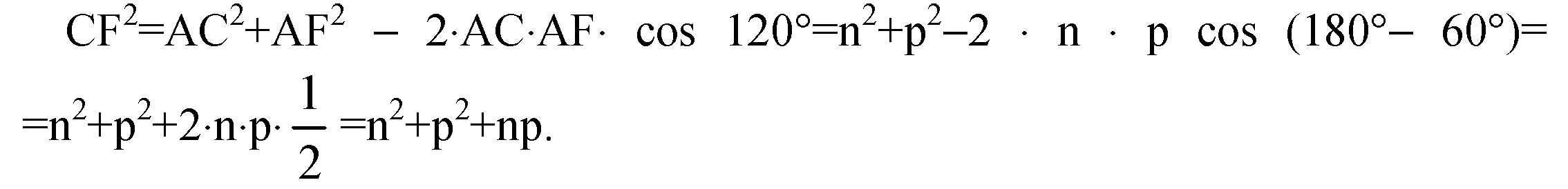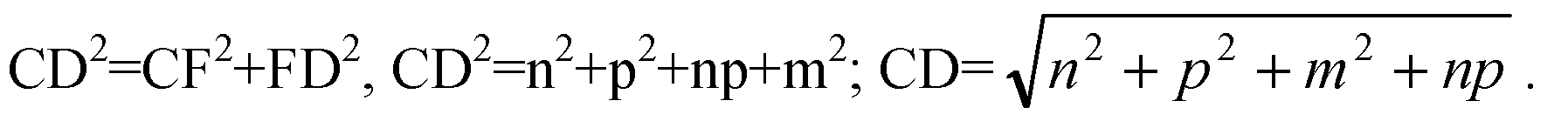516. Дан двугранный угол CABD, равный φ (φ Дополнительные задачи к главе V Метод координат в пространстве → номер 516 СА ⊥ АВ. Из А проведем прямую ОА ⊥ АВ, ∠CAO=φ. Отложим АС=АО; построим отрезок СО, из точки О проведем луч, пересекающий луч AD в точке D, OD || АВ. OD || АВ, а ОА ⊥ АВ, значит, OD ⊥ OA. По теореме о трех перпендикулярах: CO⊥OD. Обозначим AD=а. Тогда в ΔAOD: AO=a sin Θ, OD=a cos Θ. Из ΔOАС по теореме косинусов: В прямоугольном ΔCOD В ΔCAD по теореме косинусов искомый ∠CAD=х; Следовательно, 517. Отрезки СА и DB перпендикулярны к ребру двугранного угла CABD, равного 120°. Известно, что АВ=m, СА = n, BD = p. Найдите CD
Дополнительные задачи к главе V Метод координат в пространстве → номер 517
Через D проведем прямую, параллельно ребру АВ; через точку А проведем прямую, перпендикулярную ребру АВ; эти прямые пересекаются в точке F.
Тогда AF ⊥ FD. Проведем отрезок СF и отрезок CD. По теореме о трех перпендикулярах CF ⊥ FD, а значит ΔCFD — прямоугольный.
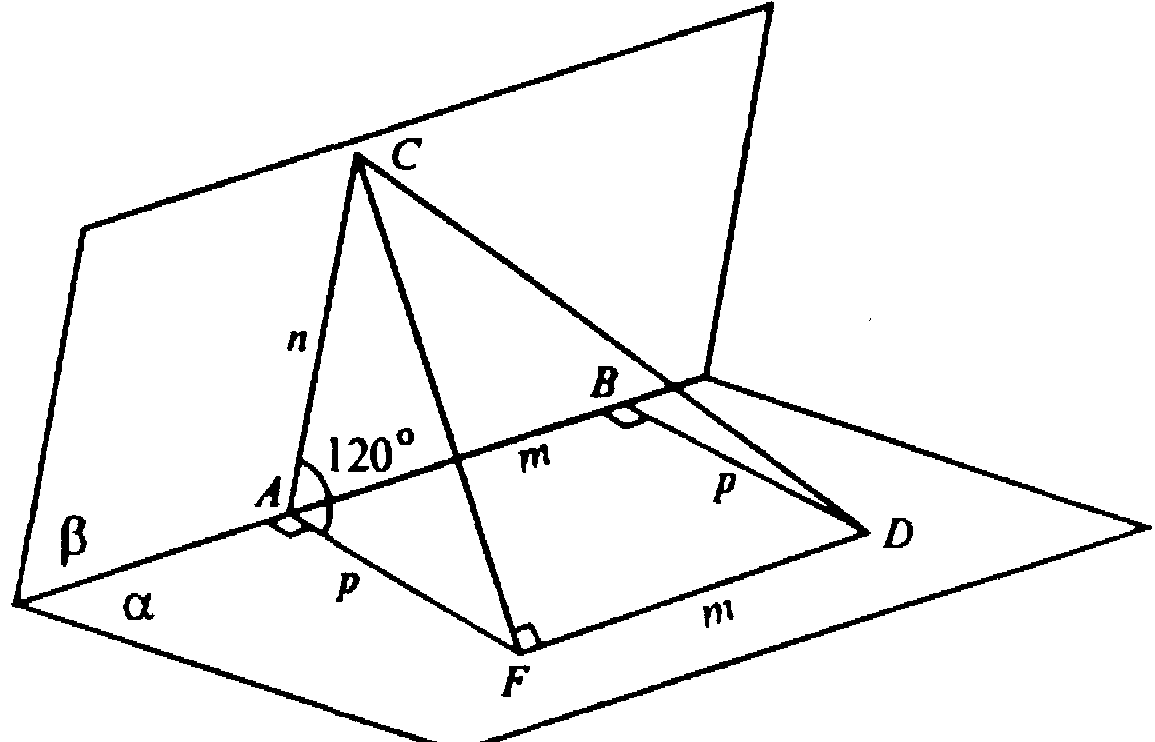
AFDB — прямоугольник,
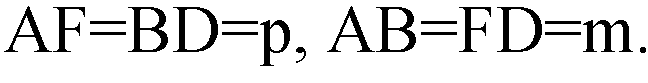
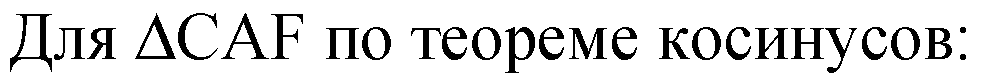
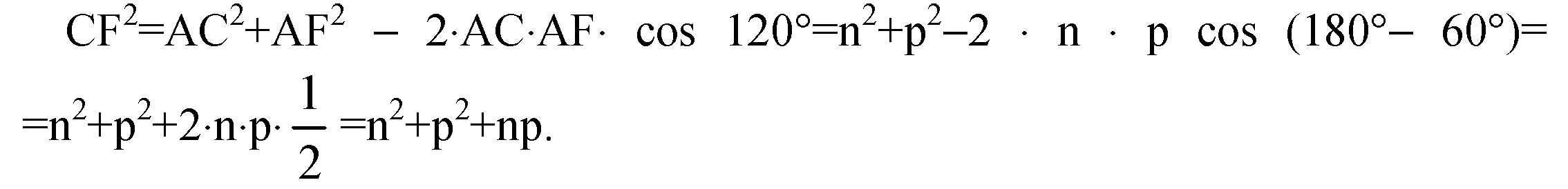
В ΔСFD: