Дополнительные задачи к главе V Метод координат в пространстве → номер 518 518. При движении прямая а отображается на прямую а1, а плоскость α — на плоскость α1. Докажите, что: а) если a||α, то a1||α1; б) если a⊥α, то a1⊥α1.
а) по условию а || α, тогда все точки прямой находятся на одинаковом расстоянии от плоскости α. Предположим, что при движении а1 не параллельна α1, т. е. а1 пересекает α1, тогда точки прямой а1 находятся на различных расстояниях от плоскости α1, что противоречит тому, что при движении расстояние между точками сохраняется. Предположение неверно, т. е. а1 || α1.
Б) Дано:
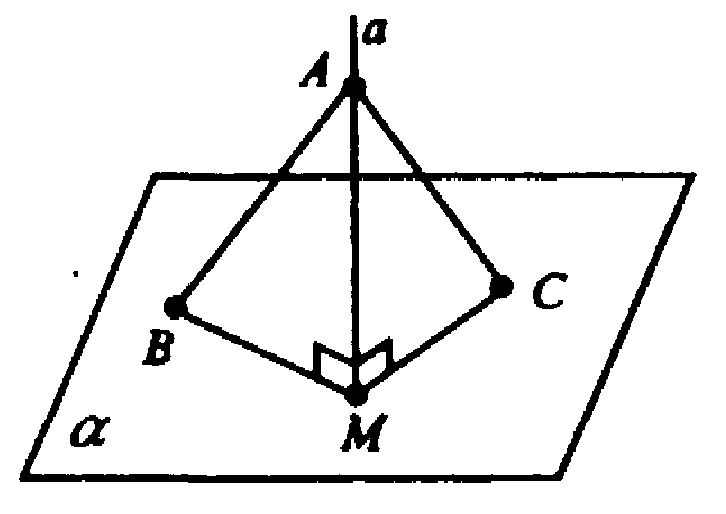
В результате движения:
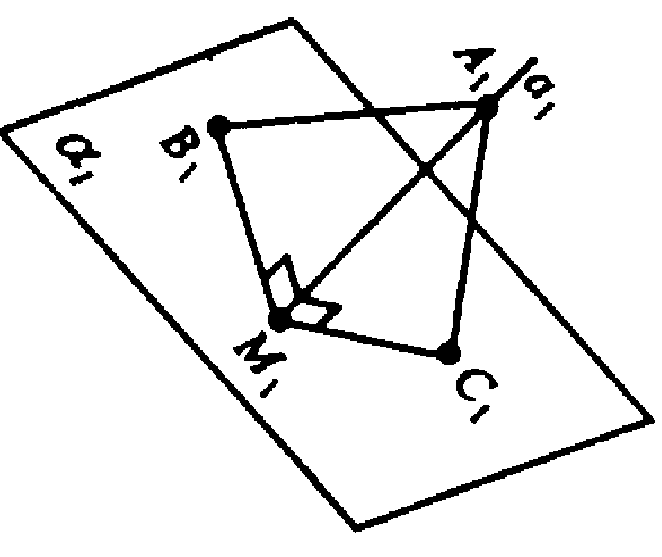
Пусть М — точка плоскости α, в которой a пересечет α. Возьмем произвольные точки
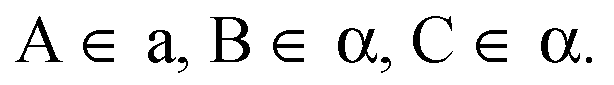
ΔAMB и ΔAMC — прямоугольные треугольники;
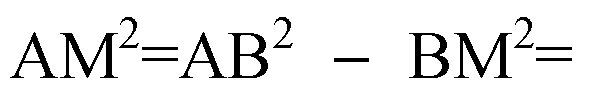
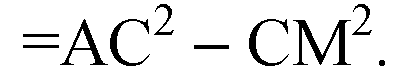
При движении
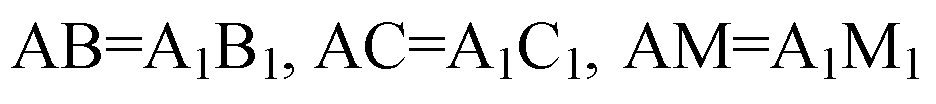
(по доказанному в преды
Дущих задачах).
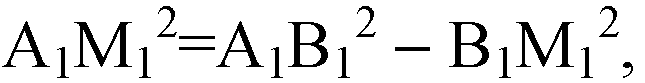
Значит,
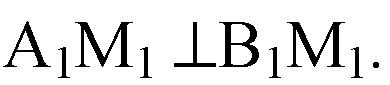
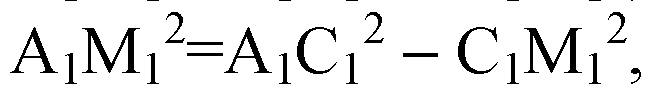
Значит,
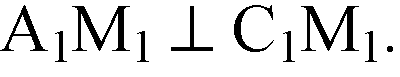
Таким образом, А1М1 перпендикулярна плоскости α1 по признаку перпендикулярности прямой к плоскости.
