Глава VI. Цилиндр, конус и шар § 3. Сфера → номер 583
Равнобедренный ΔPQR «положили» на сферу, он касается сферы в точках А, В, С. Проведем из центра сферы О перпендикуляр ОО1 на плоскость PQR.
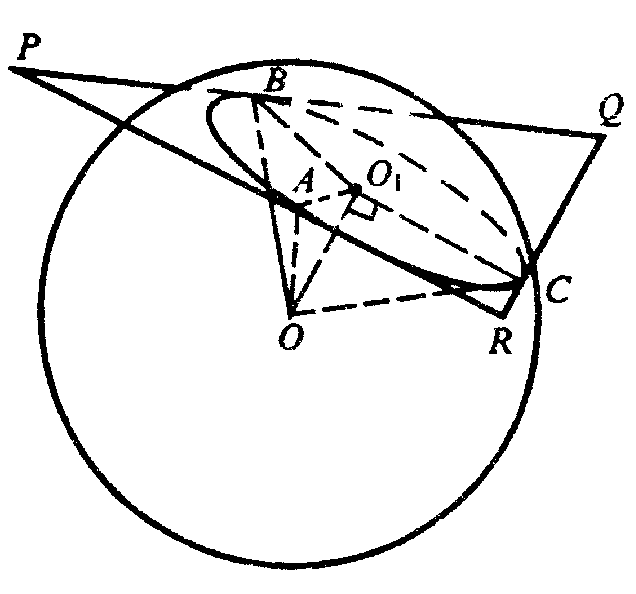
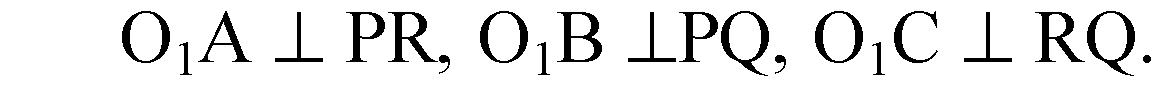
(По теореме о трех перпендикулярах О1А, О1В, О1С перпендикулярны к сторонам треугольника PQR).
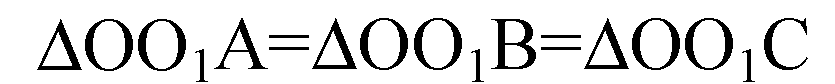
(прямоугольные, где О1О
— общий катет, ОА=ОВ=ОС=R).
Тогда: точка О1 — центр вписанной окружности.
Вычислим радиус вписанной окружности:
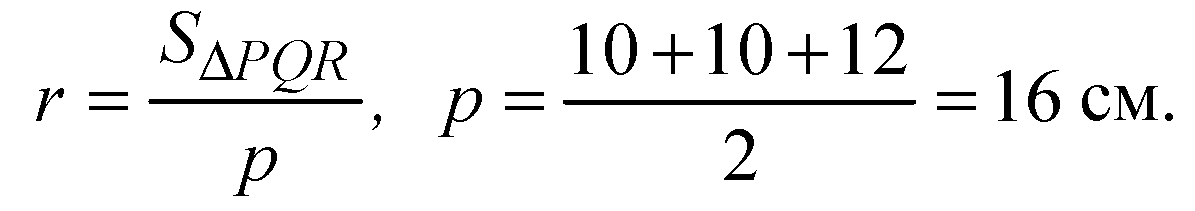
По формуле Герона:
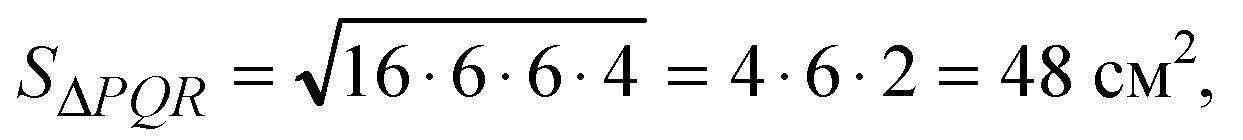
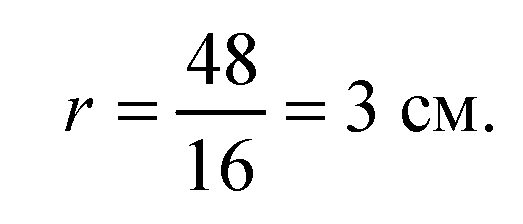
По теореме Пифагора из ΔОО1В найдем ОО1: