Глава VI. Цилиндр, конус и шар. Дополнительные задачи → номер 623
Найдите радиус сечения сферы х2+у2+z2=36 плоскостью, проходящей через точку М (2; 4; 5) и перпендикулярной к оси абсцисс.
Т. к. плоскость проходит через точку М (2; 4; 5) перпендикулярно оси абсцисс, то все точки этой плоскости имеют координаты вида (2; у; z), если они удовлетворяют уравнению х2+у2+z2=36, то будут лежать на сфере.
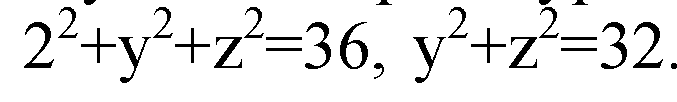
В плоскости, перпендикулярной оси абсцисс, это уравнение окружности с радиусом
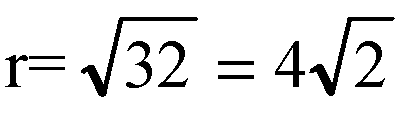
Следовательно, плоскость пересекает сферу по окружности с радиусом 4√2 .
