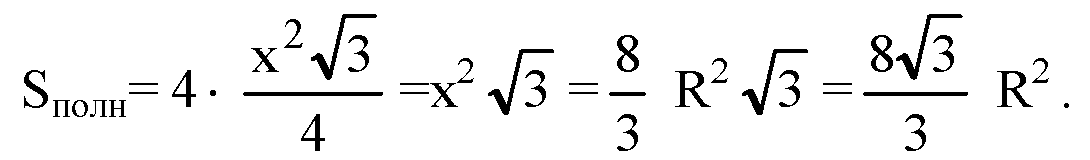Разные задачи на многогранник, цилиндр, конус и шар → номер 639
а) Центр сферы совпадает с центром куба — точкой пересечения диагоналей куба.
Пусть
Сторона основания и (его ребро) равно х. Тогда диагональ куба
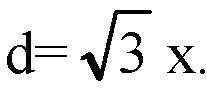
С другой стороны,
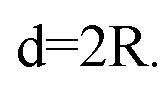
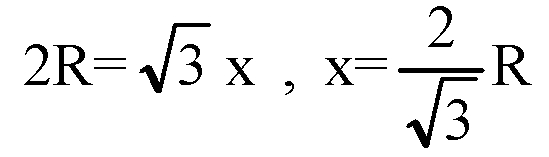
Площади поверхностей одной
Грани равна х2, а полная поверхность куба равна 6х2.
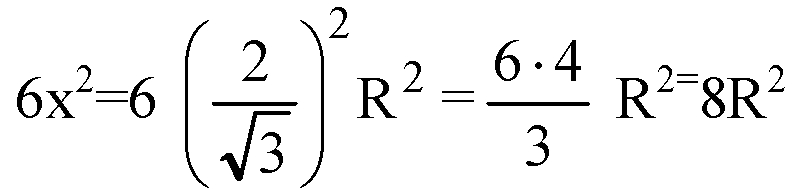
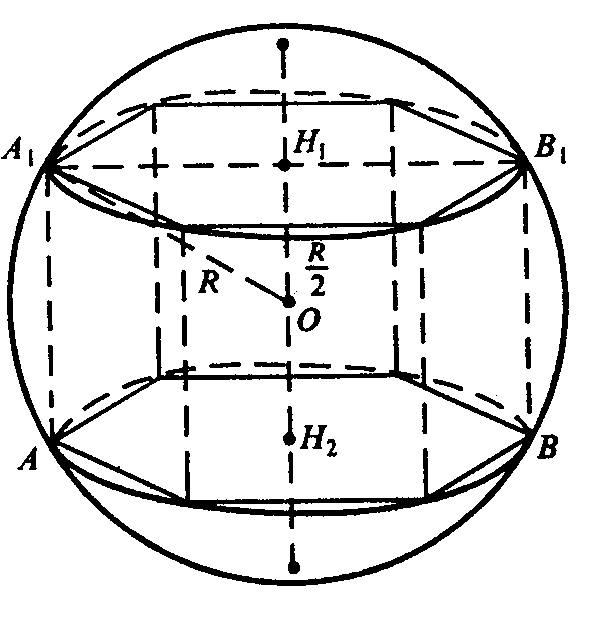
Б) Н1 и Н2 — центры оснований призмы; Н1Н2 — высота призмы. Рассмотрим сечение призмы плоскостью, проходящей через диаметр оснований призмы. Сечение является прямоугольником АА1В1В.
Из прямоугольного ΔОА1Н1:
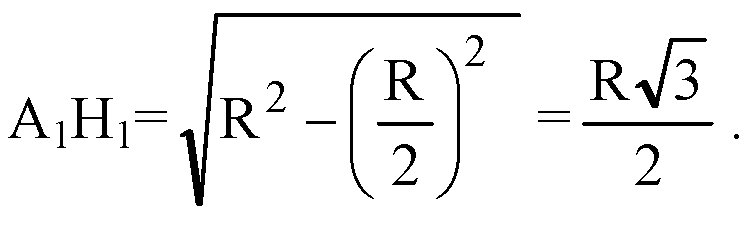
А1Н1 является радиусом описанной окружности около основания призмы, а в правильном 6-угольнике его сторона равна радиусу описанной окружности.
Пусть сторона основания равна х, следовательно,
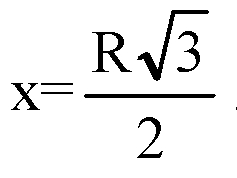
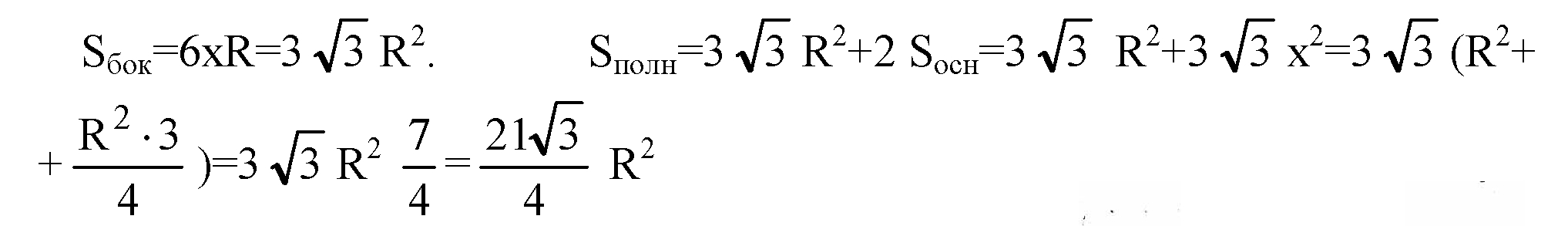
В) Пусть ребро тетраэдра равно х. Центр описанной сферы лежит на высоте DH, точка Н —
Центр ΔАВС, поэтому
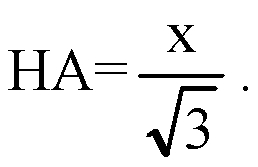
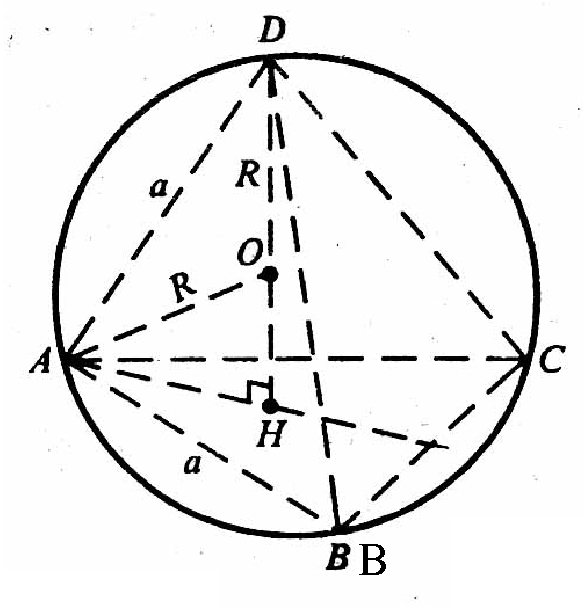
Из прямоугольного ΔАDH:
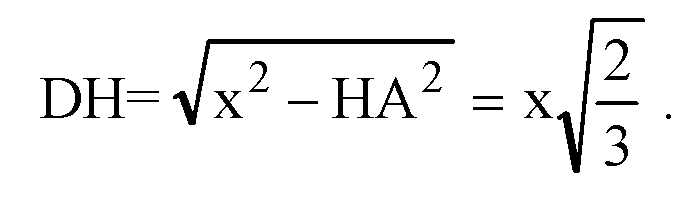
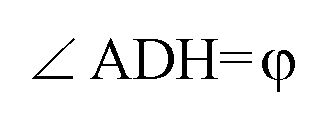
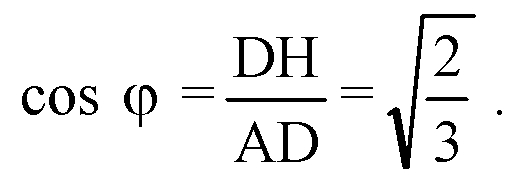
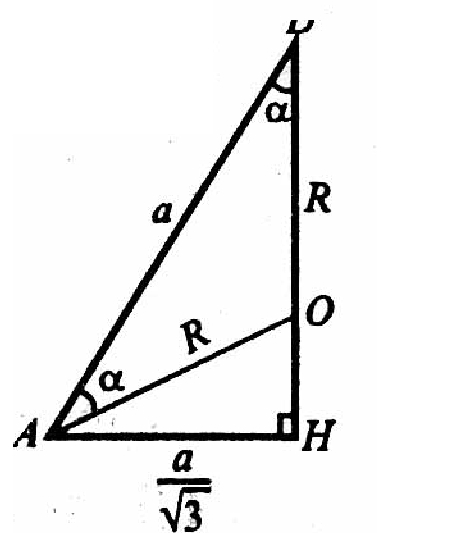
Из ΔАОD по теореме косинусов :
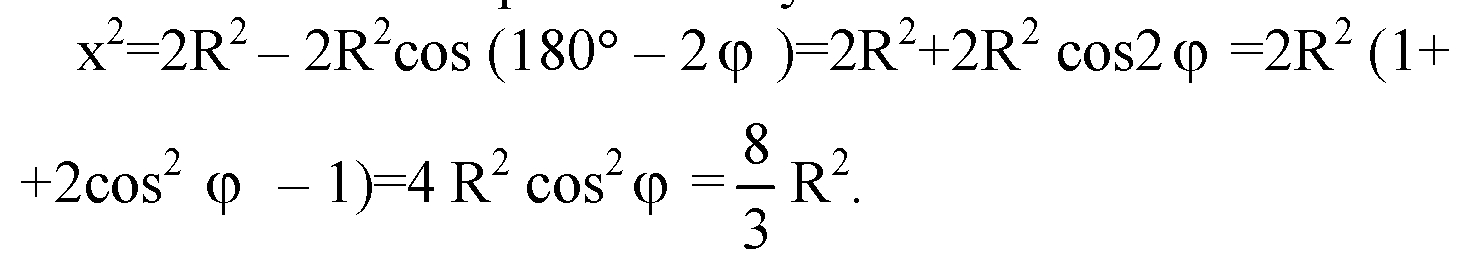
Площадь грани тетраэдра равна
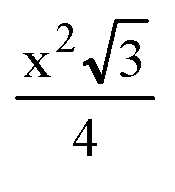
Равны и их H,
Значит