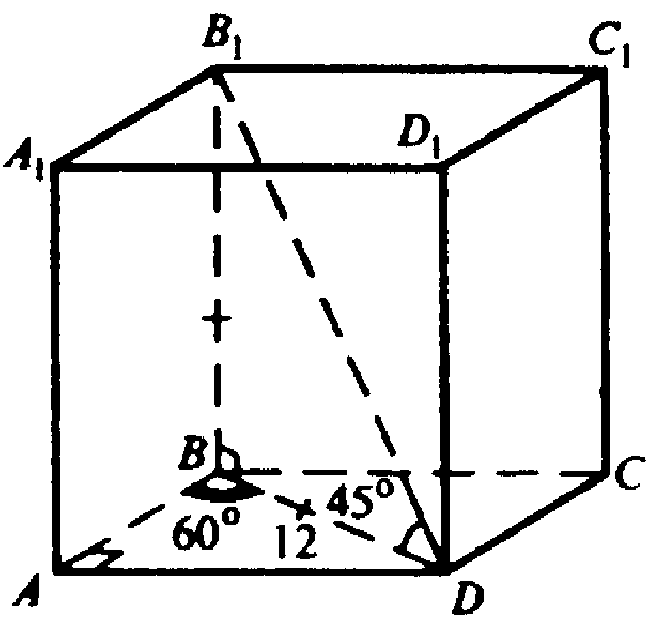
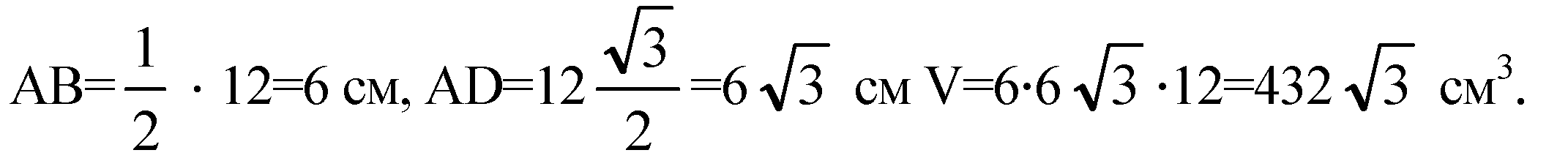Глава VII. Объемы тел. § 1. Объём прямоугольного параллелепипеда → номер 656 656. В прямоугольном параллелепипеде ABCDA1B1C1D1 диагональ B1D составляет с плоскостью основания угол в 45°, а двугранный угол A1B1BD равен 60°. Найдите объем параллелепипеда, если диагональ основания равна 12 см.
Диагонали в прямоугольнике равны, АС=BD=12 см. А1В1||АВ, АВ⊥В1В и BD⊥B1B, ∠ABD=60° — линейный угол двугранного угла
A1B1BD.
Из ΔB1BD:
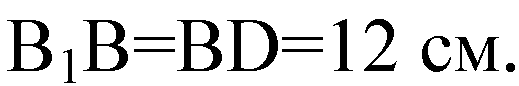
Из ΔABD: