Задачи повышенной трудности → номер 775
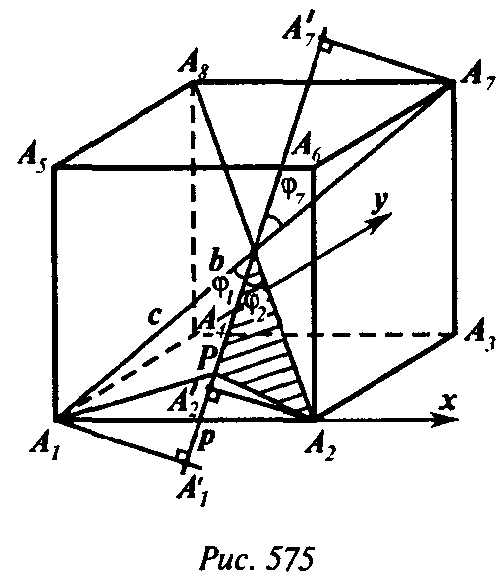
Пусть A1A2…A8 — данный куб с ребром а, р — прямая, проходящая через его центр О,
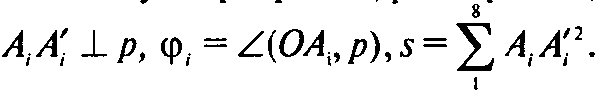
Так как
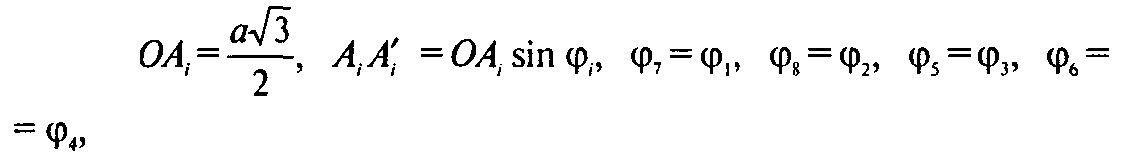
То
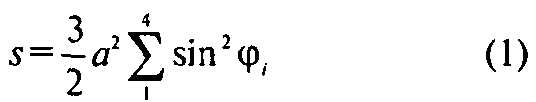
Если
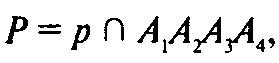
А х, у —
Координаты в системе с осями А1А2 и А1А4, то
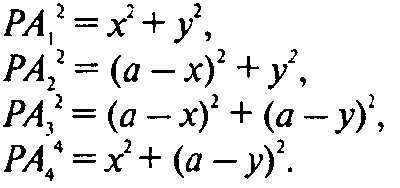
По теореме косинусов из ΔOPAi имеем
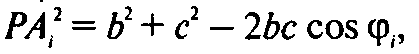
Где
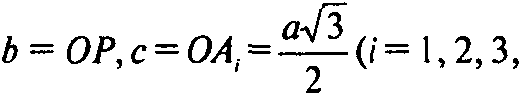
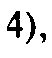
Причем
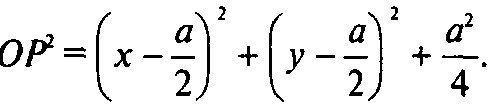
Приравняв выражения для
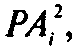
Получим из найденных
Равенств:
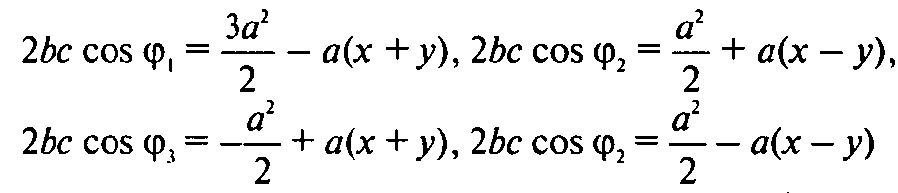
Отсюда после вычислений получаем:
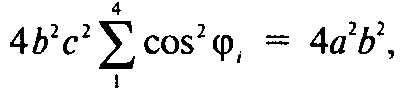
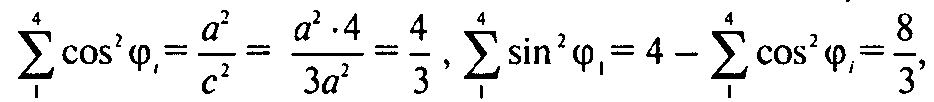
Тогда из (1)
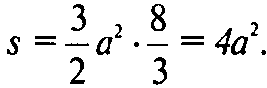
Таким образом, s не зависит от положения прямой р.
