774. Докажите, что сечением куба может быть правильный треугольник, квадрат, правильный шестиугольник, но не может быть правильный пятиугольник и правильный многоугольник с числом сторон более шести

Задачи повышенной трудности → номер 774

Если ABCDA1B1C1D1— куб с ребром a, то его сечение ACD1 — правильный треугольник, а любое сечение — параллельное грани — квадрат (рис. 574).

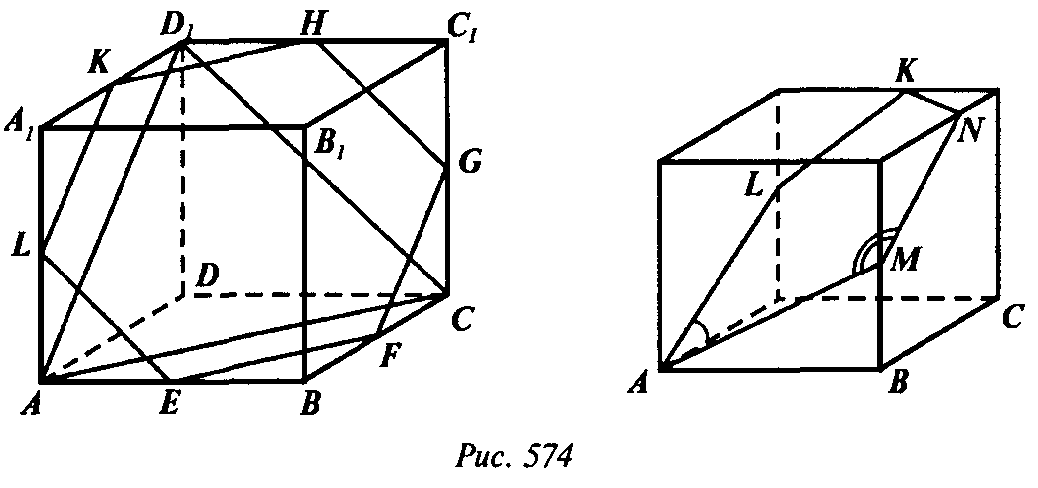
Проведем через середину Е ребра АВ плоскость α || ACD1 Она пересечет ВС в некоторой точке F.

Так как EF || АС, то по теореме Фалеса F — середина ВС и

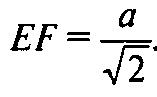
Рассуждая аналогично, получим последовательно, что α

Пройдет также через середины G, Н, К, L ребер куба, и все стороны шестиугольника EFGHKL равны

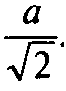
Его углы равны между собой

Как соответственные углы треугольников KLE, LEF, EFG, FGH, GHK, HKL, равных друг другу по трем сторонам.

Таким образом — сечение — правильный шестиугольник. Пятиугольное сечение правильным быть не может. Так как в сечении AMNKL AL || MN, то

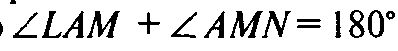
Если эти углы

Равны, то они — прямые и не равны 108°.

Сечений с семью и более сторонами быть не может, так как граней у куба только шесть.