Глава I Параллельность прямых и плоскостей. §4 Тетраэдр и параллелепипед. → номер 87 87. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью MNK, где точки М, N и К лежат соответственно на ребрах: а) ВВ1, АА1, AD1 б) СС1, AD, ВВ1.
А)
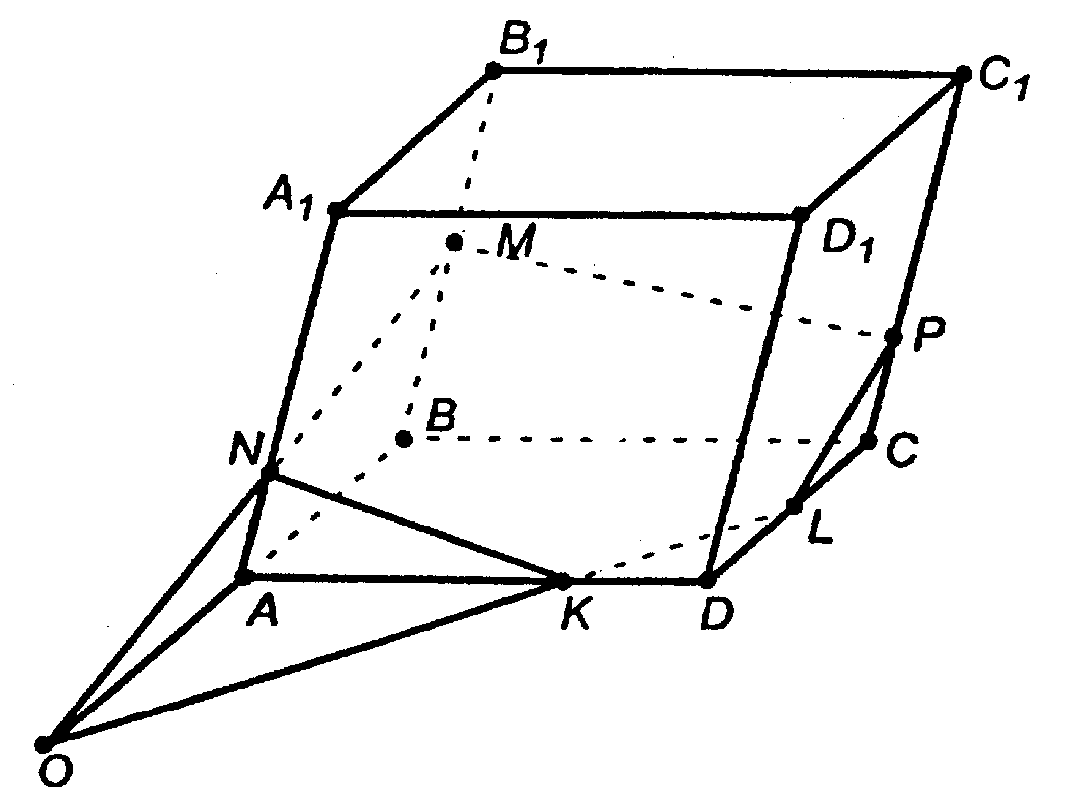
Построение
1. Допустим, что MN не параллельна АВ.
2. Продолжим MN и АВ до пересечения их в т. О.
3. ОК ⊂ пл. АВС (т. к. О ∈ АВС и K ∈ АВС).
4. Соединим точки K и N.
5. Плоскости ONK и ОАK (то есть пл. АВС) пересекаются по прямой OK.
6. Поэтому продолжим OK до пересечения с DC в т. L. Соединим точки K и L — ведь они лежат в одной плоскости.
7. Противоположные грани АА1В1В и DD1C1C секущая плоскость пересечет по параллельным прямым (по теореме II), поэтому в плоскости DD1C1C проведем LP || NM.
8. Соединим т. Р и т. М.
9. MNKLP — искомое сечение.
Б)
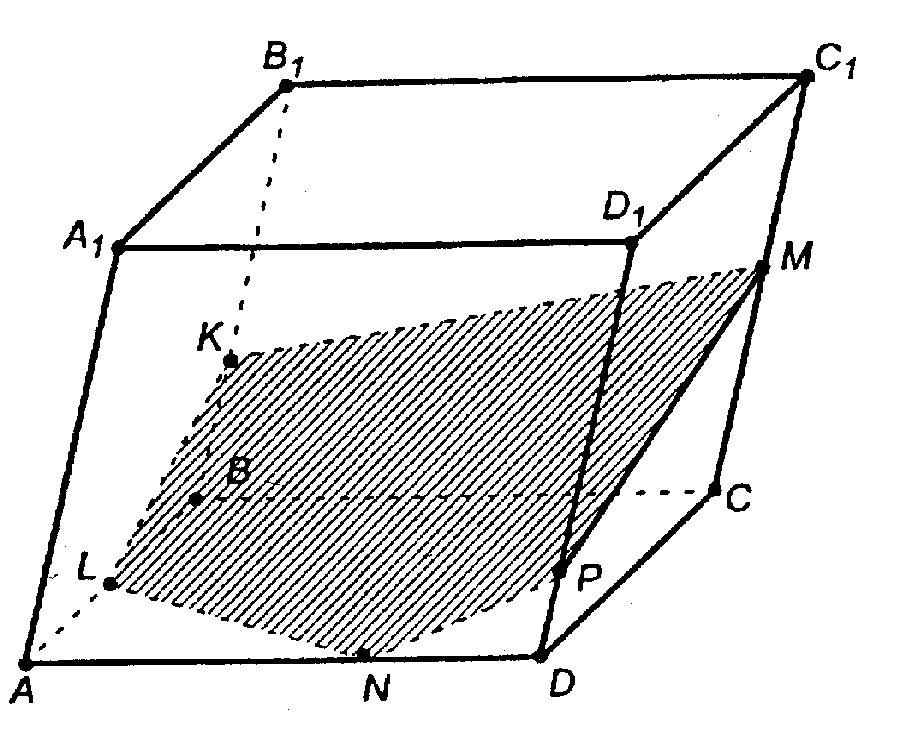
Построение
1. Соединим т. K с т. М.
2. Точка N ∈ грани AA1D1D и секущей плоскости.
3. Секущая плоскость, проходя через т. N, пересечет параллельные грани AA1D1D и ВВ1С1С по параллельным прямым; поэтому в пл. AA1D1D проводим NP || KM.
4. Проводим РМ.
5. Секущая плоскость проходит через т. K и пересекает противоположные грани АА1В1В и DD1C1C по параллельным прямым; поэтому в пл. грани АА1В1В проводим KL || MP.
6. Соединим т. L и т. N.
7. KLNPM — искомое сечение.
