Вопросы к главе VI Цилиндр, конус и шар 1. Чему равен угол между плоскостью основания цилиндра и плоскостью, проходящей через образующую цилиндра?
90 ° .
2. Что представляет собой сечение цилиндра плоскостью, параллельной его образующей?
Сечение — прямоугольник.
3. На основаниях цилиндра взяты две не параллельные друг другу хорды. Может ли кратчайшее расстояние между точками этих хорд быть: а) равным высоте цилиндра; б) больше высоты цилиндра; в) меньше высоты цилиндра?
АВ и CD лежат в параллельных плоскостях.
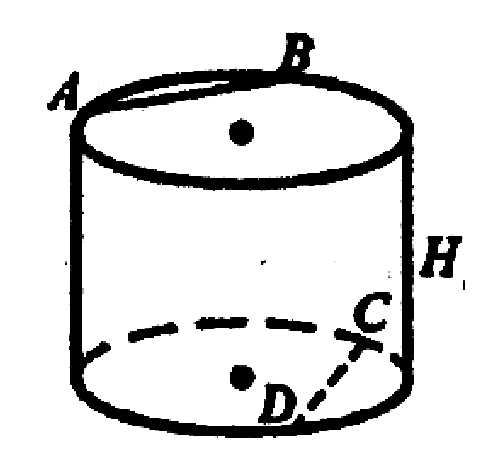
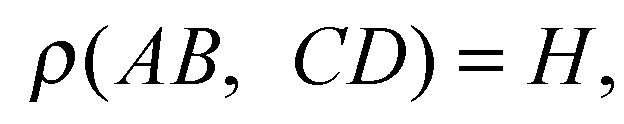
Н — высота цилиндра.
4. Две цилиндрические детали покрываются слоем никеля одинаковой толщины. Высота первой детали в два раза больше высоты второй, но радиус ее основания в два раза меньше радиуса основания второй детали. На какую из деталей расходуется больше никеля?
Первая деталь Вторая деталь
2l, l — высота (образующая),
R/2, r — радиус основания,
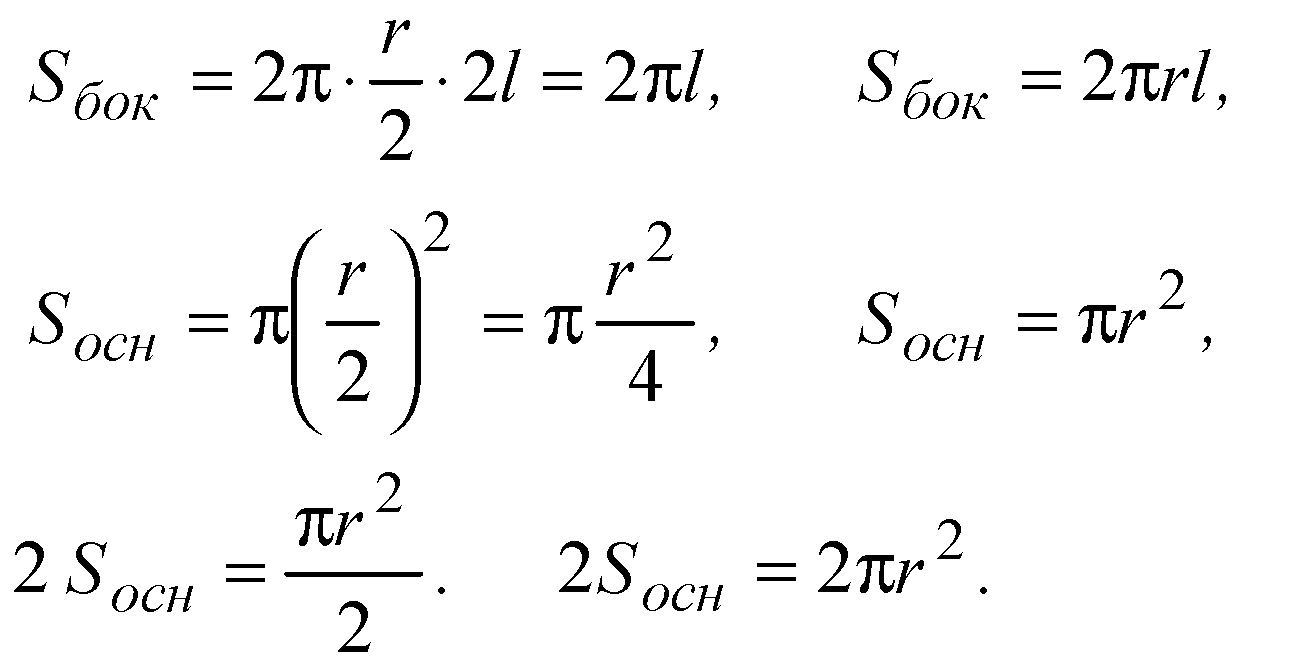
Боковые поверхности равны, но площадь двух оснований второй детали больше площади двух оснований первой детали.
5. Равны ли друг другу углы между образующими конуса и: а) плоскостью основания; б) его осью?
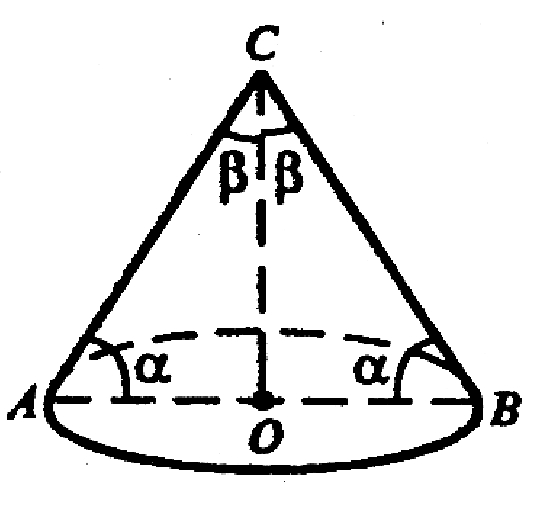
А) да; б) да.
6. Что представляет собой сечение конуса плоскостью, проходящей через его вершину?
Равнобедренный треугольник.
7. Точки А и В принадлежат шару. Принадлежит ли этому шару любая точка отрезка АВ?
Да.
8. Могут ли все вершины прямоугольного треугольника с катетами 4 см и 2 √2 см лежать на сфере радиуса √5 см?
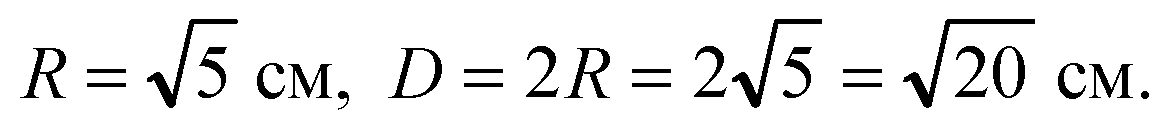
Вычислим гипотенузу прямоугольного треугольника:
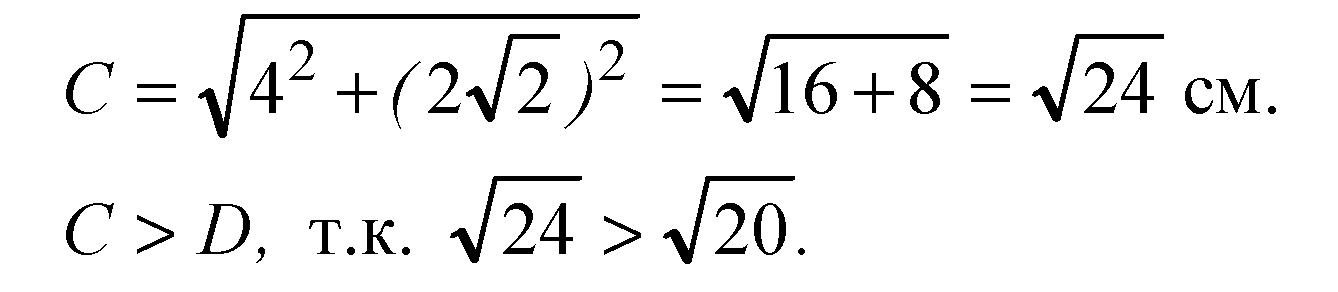
Гипотенуза не помещается внутри сферы, тогда, хотя бы одна вершина лежит вне сферы.
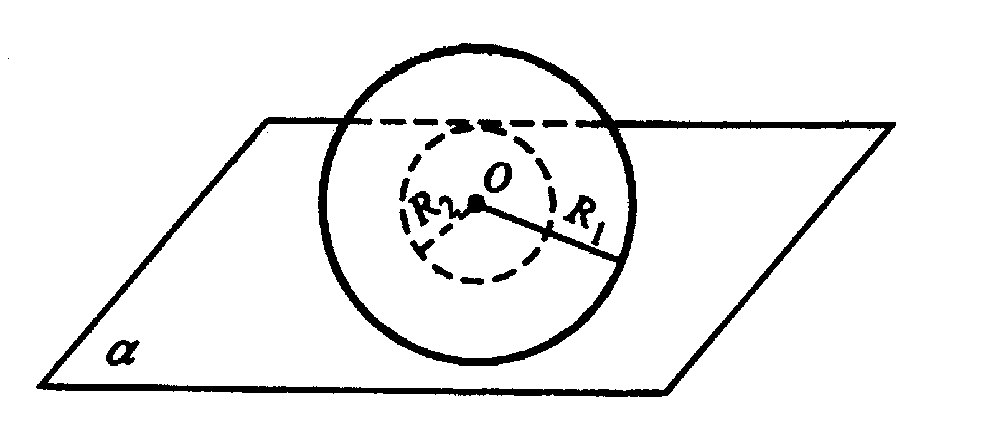
9. Могут ли две сферы с общим центром и с неравными радиусами иметь общую касательную плоскость?
Одна сфера всегда будет внутри другой, поэтому общую касательную плоскость провести невозможно.
10. Что представляет собой множество всех точек пространства, из которых данный отрезок виден под прямым углом?
Это сфера, у которой данный отрезок является диаметром.
