Вы предлагаете товарищу задумать любое трехзначное число, не оканчивающееся нулем (но такое, чтобы разница между крайними цифрами была не меньше 2), и просите затем переставить цифры в обратном порядке. Сделав это, он должен вычесть меньшее число из большего и полученную разность сложить с нею же, но написанною в обратной последовательности цифр. Ничего не спрашивая у загадчика, вы сообщаете ему число, которое у него получилось в конечном итоге.
Если, например, было задумано 467, то загадчик должен выполнить следующие действия:
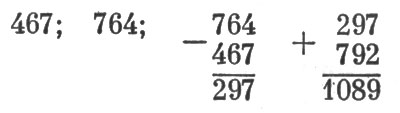
Этот окончательный результат — 1089 — вы и объявляете загадчику. Как вы можете его узнать?
Рассмотрим задачу в общем виде. Возьмем число с цифрами а, b, с, причем а больше чем с по крайней мере на две единицы. Оно изобразится так:
100a + 10b + c
Число с обратным расположением цифр имеет вид:
100c + 10b + a
Разность между первым и вторым равна:
99a - 99c.
Делаем следующие преобразования:
99a - 99c = 99(a - c) = 100(a - c) - (a - c) = 100(a - c) - 100 + 100 - 10 + 10 - a + c = 100 (a - c - 1) + 90 + (10 - a + c)
Значит, разность состоит из следующих трех цифр:
- Цифра сотен: a — c — 1,
- Цифра десятков: 9,
- Цифра единиц: 10 + c — a.
Число с обратным расположением цифр изображается так:
100(10 + c - a) + 90 + (a - c - 1)
Сложив оба выражения
100(a - c - 1) + 90 + 10 + c - a
+
100(10 + c - a) + 90 + a - c - 1,
Получаем
100×9 + 180 + 9 = 1089.
Итак, независимо от выбора цифр a, b и с всегда получается одно и то же число: 1089. Нетрудно поэтому отгадать результат этих вычислений: вы знали его заранее.
Понятно, что показывать этот фокус одному лицу дважды нельзя — секрет будет раскрыт.
