121. Так как сумма всех чисел, обозначенная на циферблате, равна 78, то числа каждого из шести участков должны составлять вместе 78 : 6, т. е. 13. Это облегчает отыскание решения, которое показано на рис. 101.
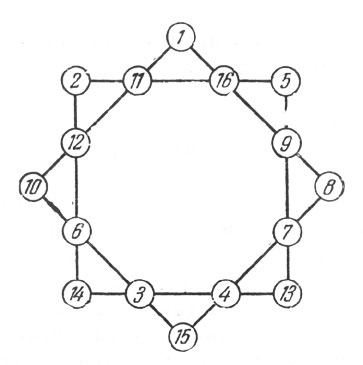
Рис. 102. Решение задачи 122
122-123. Решения показаны на прилагаемых рис. 102 и 103.
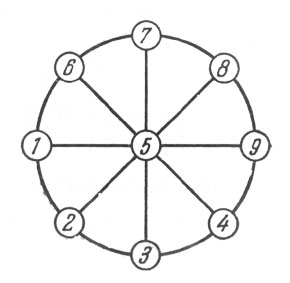
Рис. 103. Решение задачи 123
124. Трехногий стол всегда может касаться пола концами своих трех ножек, потому что через каждые три точки пространства может проходить плоскость и притом только одна; в этом причина того, что трехногий стол не качается. Как видите, она чисто геометрическая, а не физическая.
Вот почему так удобно пользоваться треногами для землемерных инструментов и фотографических аппаратов. Четвертая нога не сделала бы подставку устойчивее; напротив, пришлось бы тогда всякий раз заботиться о том, чтобы подставка не качалась.
125. На вопрос задачи легко ответить, если сообразить, какое время показывают стрелки. Стрелки в левом кружке (рис. 96) показывают, очевидно, 7 час. Значит, между концами этих стрелок заключена дуга в 5/12 полной окружности.
В градусной мере это составляет
360° х 5/12 = 150°.
Стрелки в правом кружке показывают, как нетрудно сообразить, 9 ч. 30 м. Дуга между их концами содержит 3 1/2 двенадцатых доли полной окружности или 7/24.
В градусной мере это составляет
360° х 7/24 = 105°.
L26. Принимая рост человека в 175 см и обозначив радиус Земли через R, имеем:
2 х 3,14 х(R + 175) - 2 х 3,14 х R = 2 x 3,14 x 175 = 1100 см,
Т. е. около 11 м. Поразительно здесь то, что результат совершенно не зависит от радиуса шара и, следовательно, одинаков на исполинском Солнце и маленьком шарике.
127. Требованию задачи легко удовлетворить, если расставить людей в форме шестиугольника, как показано на рис. 104.

Рис. 104. Требованию задачи легко удовлетворить, если расставить людей в форме шестиугольника
