Читатели, слыхавшие о неразрешимости задачи квадратуры круга, сочтут, вероятно, и предлагаемую задачу неразрешимой строго геометрически. Раз нельзя превратить в равновеликий квадрат полный круг, то — думают многие — нельзя превратить в прямоугольную фигуру и луночку, составленную двумя дугами окружности.
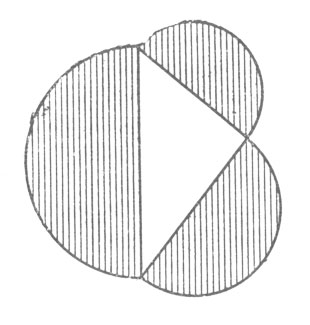
Рис. 105. Сумма площадей полукругов, построенных на катетах, равна полукругу, построенному на гипотенузе
Между тем, задача, безусловно, может быть решена геометрическим построением, если воспользоваться одним любопытным следствием общеизвестной Пифагоровой теоремы. Следствие, которое я имею в виду, гласит, что сумма площадей полукругов, построенных на катетах, равна полукругу, построенному на гипотенузе (рис. 105). Перекинув большой полукруг на другую сторону (рис. 106), видим, что обе заштрихованные луночки вместе равновелики треугольнику*. Если треугольник взять равнобедренный, то каждая луночка в отдельности будет равновелика половине этого треугольника (рис. 107).
* (Положение это известно в геометрии под названием теоремы о гиппократовых луночках.)
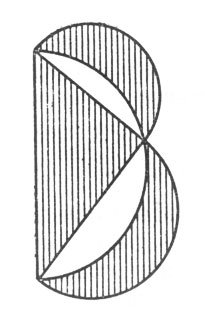
Рис. 106. Перекинув большой полукруг на другую сторону, видим, что обе заштрихованные луночки вместе равновелики треугольнику
Отсюда следует, что можно геометрически точно построить равнобедренный прямоугольный треугольник, площадь которого равна площади серпа.
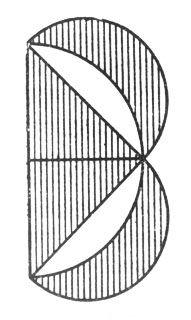
Рис. 107. Если треугольник взять равнобедренный, то каждая луночка в отдельности будет равновелика половине этого треугольника
А так как равнобедренный прямоугольный треугольник превращается в равновеликий квадрат (рис. 108), то и серп наш возможно чисто геометрическим построением заменить равновеликим квадратом.
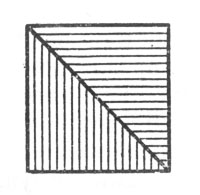
Рис. 108. Равнобедренный прямоугольный треугольник превращается в равновеликий квадрат
Остается только превратить этот квадрат в равновеликую фигуру Красного креста (составленную, как известно, из пяти примкнутых друг к другу равных квадратов).
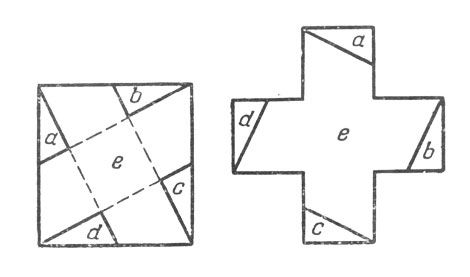
Рис. 109. Существует несколько способов выполнения такого построения
Существует несколько способов выполнения такого построения; два из них показаны на рис. 109 и 110; оба построения начинают с того, что соединяют вершины квадрата с серединами противоположных сторон.
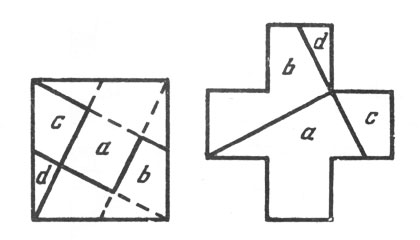
Рис. 110. Существует несколько способов выполнения такого построения
Важное замечание: превратить в равновеликий крест можно только такую фигуру серпа, которая составлена из двух дуг окружностей: наружного полукруга и внутренней четверти окружности соответственно большего радиуса*.
* (Тот лунный серп, который мы видим на небе, имеет несколько иную форму: его наружная дуга — полуокружность, внутренняя же — полуэллипс. Художники часто изображают лунный серп неверно, составляя его из дуг окружностей.)
Итак, вот ход построения креста, равновеликого серпу. Концы А и В серпа (рис. 111) соединяют прямой; в середине О этой прямой восставляют перпендикуляр и откладывают ОС = ОА. Равнобедренный треугольник ОАС дополняют до квадрата OADC, который превращают в крест одним из способов, указанных на рис. 109 и 110.
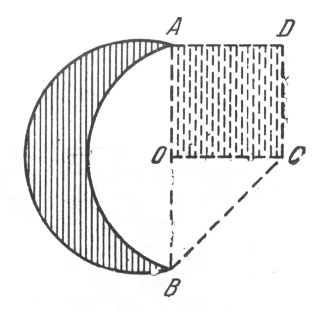
Рис. 111. Ход построения креста, равновеликого серпу
