129. Указанная дополнительная возможность не облегчает задачу: все равно требуется шесть разрезающих плоскостей. В самом деле, внутренний кубик из числа тех 27, на которые надо разрезать большой куб, имеет шесть граней, и никакая разрезающая плоскость не может открыть сразу двух граней этого внутреннего кубика, как бы мы ни переставляли части.
130. Сначала посмотрим, каково может быть наименьшее число разрезов. Если мы провели один разрез, то доска распадается на две части. Следующим разрезом, если он рассечет обе из них, мы получим 4 части. Если мы расположим их так, что третий разрез пересечет их все, то число частей снова удвоится, и после третьего разреза мы получим 8 частей. После четвертого разреза мы получим самое большее 16 частей (если разрез пересечет все получившиеся ранее части), после пятого — 32 части. Значит после пяти разрезов мы никак еще не сможем получить 64 отдельных квадратика. И лишь после шестого разреза, когда число частей опять удвоится, мы можем рассчитывать получить 64 отдельных квадратика. Значит менее чем шестью разрезами обойтись невозможно.
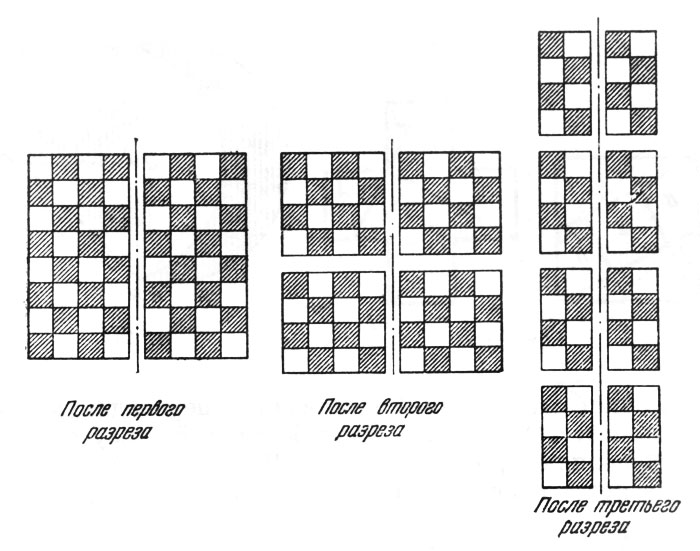
Рис. 112. Первые три разреза
Но теперь надо еще показать, что шесть разрезов можно в действительности осуществить так, чтобы каждый раз число частей удваивалось и в результате получилось 26 = 64 отдельных квадратика. Это уже нетрудно сделать: надо только следить, чтобы после каждого разреза все части оказывались равными и чтобы каждый очередной разрез разбивал каждую из частей пополам. На рис. 112 показаны первые три разреза.
