Можно ли совершить переправу при тех же условиях, если к реке подъехали четыре рыцаря с оруженосцами?
Решение. Четыре рыцаря со своими оруженосцами не смогут переправиться с первого берега на второй, соблюдая условия задачи. Чтобы объяснить это, предположим, что переправа возможна, и перенумеруем, начиная с первого, все рейсы, которые совершит лодка. Тогда после нечетных рейсов она будет находиться на втором берегу, а после четных — на первом. Обозначим через 2k + 1 наименьший номер нечетного рейса, в результате которого на втором берегу окажется более двух рыцарей. Рейс с номером 2k + 1 может доставить на второй берег не более двух человек, поэтому после рейса 2k — 1 на втором берегу должен находиться по крайней мере один рыцарь. Мы видим, что после рейса 2k — 1 на втором берегу могут находиться или один, или два рыцаря.
В первом случае обозначим рыцарей, оставшихся на первом берегу, через A, В, С, а рыцаря на втором берегу — через D. Если соответствующих оруженосцев обозначить а, b, с, d, то с соблюдением условий задачи возможно единственное распределение оруженосцев. Итак, в первом случае после рейса с номером 2k — 1 мы получим такую картину:
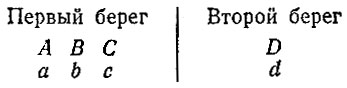
Кто же отправится в лодке рейсом 2k? Рыцарь D уплыть им не может, ведь тогда после рейса 2k + 1 на втором берегу будет не более двух рыцарей. Значит, рейсом 2k поплывет один оруженосец d, но тогда на первом берегу он окажется в обществе чужих рыцарей, что противоречит условию задачи. В рейс 2k плыть некому. Это означает, что первый случай невозможен.
Во втором случае обозначим рыцарей на первом берегу через Л, В и переправившихся рыцарей через С, D. Тогда после рейса 2k — 1 имеем:

Кто же в этом случае отправится рейсом 2k? Ни один из рыцарей С, D уплыть не может, так как тогда рейсом 2k + 1 с первого берега должны плыть два рыцаря и один из оруженосцев а или b остается без, охраны. Но ни один из оруженосцев с, d не может плыть рейсом 2k без своего рыцаря, ведь на первом берегу находятся А, В. Опять в рейс 2k плыть некому. Итак, мы установили, что с соблюдением условий задачи на второй берег не может переправиться более двух рыцарей.
