Попросите своего товарища задумать число, пусть затем он удвоит задуманное число и к полученному произведению прибавит 5. Потом пусть полученное число возьмет пять раз и прибавит к результату число 10. Эту последнюю сумму пусть он умножит еще на 10. Если после этого спросить, какое, в конце концов, получилось число, и отнять от него 350, то число оставшихся сотен и будет задуманным числом. Почему это так?
Пример. Пусть задумано 3. По удвоении его получается 6; если прибавить 5, получится 11; взять пять раз 11 — получится 55; прибавить сюда 10 — получится 65; увеличить в 10 раз — получится 650. Если отнять отсюда 350, останется 300, т. е. три сотни. Итак, задуманное число есть 3.
Решение. Над задуманным числом n совершаются следующие действия:
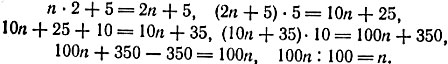
То есть всегда получится задуманное число.
Замечания. Рассматривая решение последней задачи, нетрудно понять, что ей можно придать любое число различных видоизменений. Так, например, если пожелать, чтобы всегда в результате число сотен выражало задуманное число и чтобы приходилось умножать всегда на 2, 6 и 10, но вычитать приходилось бы не 350, как в приведенной задаче, а другое число, то нужно принять во внимание, как получилось в вышеприведенной задаче 350. Это число произошло так: прибавлено 5, да умножено на 5, итого 25; к этому числу прибавлено 10, получилось 35; умножив же это число на 10, получаем 350. Следовательно, если захотеть вместо 350 вычитать из окончательного результата другое число, то и задавать нужно прибавлять не 5 и 10, а другие числа. Зададим, например, вместо 5 прибавить 4, а вместо 10 прибавить 12. Ясно, что из последнего полученного числа придется вычесть 320(4*5 = 20; 20+12 = 32; 32*10 = 320), и тогда получим остаток, число сотен которого и даст нам задуманное число. Таким образом, задачу можно видоизменять до бесконечности.
Точно так же легко заметить, что, умножая задуманное число на 2, на 5 и на 10, мы умножаем его, в сущности, на 100 (2*5*10 = 100).
Поэтому, если мы опять-таки хотим, чтобы число сотен окончательного результата показывало задуманное число,- все равно, какие множители выбрать, лишь бы умножение на них давало в окончательном результате умножение на 100. Отсюда следует, что, оставляя те же множители 2, 5, 10, можно изменить их порядок, т. е. сначала умножить, например, на 5, потом на 10, а затем на 2 и т. д.
Точно так же вместо множителей 2, 5, 10 можно брать другие, дающие в произведении 100, например: 5, 4, 5 или 2, 2, 25 и т. д. Нужно помнить только при этом, конечно, что всем этим изменениям множителей и прибавляемых чисел соответствует изменение числа, которое в конце нужно вычесть. Так, например, будем умножать на 5, 4, 5, а прибавлять числа 6 и 9, и пусть задуманное число будет 8.
Умножив на 5, получим 40; прибавив 6, получим 40 + 6 = 46; умножив на 4, получим 160 + 24 = 184; прибавив 9, получим 160 + 33 = 193; умножив это число на 5, получим 800 + 165 = 965, т. е. для получения числа сотен, показывающего задуманное число, нужно отнять в данном случае 165(6*4 = 24; 29 + 9 = 33; 33*5 = 165).
Можно также взять не 100, а любое иное число и сделать так, чтобы оно заключалось в остатке от последнего вычитания столько раз, сколько единиц заключается в задуманном числе. Так, например, возьмем число 24, которое можно представить состоящим из множителей 2, 3, 4 (2*3*4 = 24), а числа, которые будем прибавлять, пусть будут 7 и 8.
Пусть задуманное число есть 5. Удваивая его, находим 10, прибавляя 7, находим 10 + 7 = 17; утраивая, находим (10 + 7)*3 = 30 + 21 = 51; прибавляя 8, находим 30 + 29 = 59; беря последнее число 4 раза, получим 120 + 116 = 326. Отнимаем отсюда 116, остается 120, в котором 24 содержится 5 раз, т. е. по-* лучается задуманное число 5.
Можно также вместо трех множителей брать только два, а вместо двух чисел прибавлять только одно, и тогда число десятков числа, полученного после вычисления, подобного предыдущему, покажет задуманное число.
Можно также брать четыре, пять, шесть и т. д. множителей, прибавлять соответствующее (три, четыре и т. д.) количество чисел, затем, поступая, как указано выше, угадывать задуманное кем-либо число.
Можно, наконец, вместо того, чтобы прибавлять числа, вычитать их, а в конце вместо вычитания прибавлять известное число. Так, например, воспользуемся числами первого примера настоящей задачи, и пусть задуманное число будет 12. Удвоив его, получим 24; вычитая отсюда 5, получим 24-5; умножая на 5, получим 120-25; вычитая 10, получим 120-35; умножая на 10, получим 1200-350. Здесь вместо того, чтобы вычесть, нужно прибавить 350: сумма получится 1200, и число сотен в ней (12) дает задуманное число.
Словом, читатель может видоизменять и разнообразить эту задачу, как ему угодно.
