В каждой из 9 клеток квадрата (рис. 158) поставить одно из чисел 1, 2, 3 так, чтобы сумма чисел, стоящих в каждом вертикальном ряду, в каждом горизонтальном ряду, а также по любой диагонали равнялась 6. Найти все расстановки.
Рис. 158
Решение. Конечно, можно во всех клетках квадрата поставить число 2. Получившийся числовой квадрат будет удовлетворять условиям задачи.
Но, если потребовать, чтобы среди чисел было по крайней мере одно нечетное, задача становится не такой простой.
Прежде всего, сделав несколько проб, легко убедиться, что в центре квадрата не могут стоять ни 1, ни 3. Этому факту можно дать и строгое доказательство. Предположим, что числа расставлены так как требуется. Прибавим друг к другу числа, стоящие на диагоналях и во втором столбце (при этом число стоящее в центре квадрата, будет взято трижды); и вычтем из результата числа, стоящие в первой и третьей строках. Разность, как легко видеть будет равна утроенному числу из центра квадрата. С другой стороны, сумма чисел на диагоналях, в каждом столбце и в каждой строке равняется 6; значит разность должна равняться 6. Следовательно, в центре квадрата стоит число 2.
Далее, легко видеть, что сумма чисел равняется 6 только в том случае, если все они различны или все равны 2. Поэтому по крайней мере в одной из вершин квадрата должно стоять число 2. Искомые расстановки теперь легко находятся (рис. 159) Все они получаются из первой с помощью симметрии относительно диагонали (2, 2, 2), относительно второй строки " относительно второго столбца.
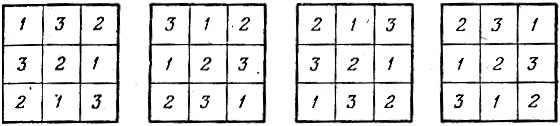
Рис. 159
Для построения нужного размещения чисел можно воспользоваться одним легко запоминающимся приемом. Расположим сначала числа так, как на рис. 160, а. Затем числа, лежащие вне квадрата ABCD, сдвигаем соответственно вниз, вверх, влево или вправо на 3 клетки так, чтобы они попали на свободные места в квадрате. Получаем в результате требуемое размещение (рис. 160, б).
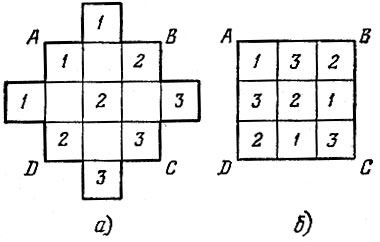
Рис. 160
