На постоялом дворе нетерпеливый проезжий, увидя кучера, спросил:
— Не пора ли запрягать?
— Что вы!- ответил кучер,- еще полчаса до отъезда. За это время я успею двадцать раз и запрячь, и отпрячь, и опять запрячь. Нам не впервой…
— А сколько в карету впрягается лошадей?
— Пять.
— Сколько времени полагается на запряжку лошадей?
— Да минуты две — не больше.
— Ой ли?- усомнился проезжий.- Пять лошадей запрячь в две минуты. Что-то уж очень скоро…
— И очень просто,- отвечал кучер.- Выведут лошадей в сбруе, постромках с вальками, в вожжах. Остается только накинуть кольца вальков на крюки, приструнить двух средних лошадей к дышлу, взял вожжи в руки, сел на козлы и готово… Поезжай! Дело знакомое…
— Ну, хорошо!- заметил пассажир.- Допустим, что таким образом можно запрячь и отпрячь лошадей хоть двадцать раз в полчаса. Но если их придется перепрягать одну на место другой, да еще всех, то уж 3того никогда не сделать не только в пол, но и в два часа.
— Тоже пустячное дело!- расхвастался кучер.- Разве нам не приходится перепрягать! Да какими угодно способами я их всех перепрягу в час, а то и меньше. Одну лошадь поставил на место другой, и готово! Минутное дело!
— Нет, ты перепряги их не теми способами, которые мне угодны,- сказал пассажир,- а всеми способами, какими только можно перепрячь пять лошадей, считая на перепряжку одну минуту, как ты хвастаешь.
Самолюбие кучера было несколько задето.
— Конечно, всех лошадей и всеми способами перепрягу не больше как за час.
— Я дал бы сто рублей, чтобы посмотреть, как ты сделаешь это за час!- сказал пассажир.
— А я при своей бедности заплачу за ваш проезд в карете, если этого не сделаю,- ответил кучер.
Так и условились. Каков был результат спора?
Решение. В пылу спора кучер не смог представить, сколь велико количество запряжек, которые он должен сделать. Подсчитаем же мы это количество.
Обозначив лошадей цифрами 1, 2, 3, 4, 5, мы должны выяснить, сколькими способами можно переставить эти пять цифр.
Две цифры можно переставить двумя способами: (1, 2) и (2, 1). Перестановок из трех 1, 2, 3, начинающихся с цифры 1, будет также две. Но это число не зависит от того, какая фиксированная цифра из трех стоит на первом месте. Значит, всего перестановок из трех цифр будет 3*2 = 6:
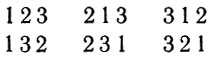
Продолжая далее, мы находим, что перестановок из четырех цифр с фиксированной первой цифрой будет б и множество всех перестановок из 4 цифр распадается на 4 группы по 6 перестановок, начинающихся с одной и той же цифры — 1, 2, 3 или 4. Так что всех перестановок будет 4*6=4*3*2*1 = 24. Аналогично, множество всех перестановок из 5 цифр состоит из 5 групп по 24 перестановки, начинающихся с одной цифры — 1, 2, 3, 4 или 5. Всего их будет 5*24 = 5-*4*3*2*1 = 120.
Можно доказать, что множество перестановок из n цифр {1, 2, 3, …, n} равняется произведению 1*2*3*…*n. Это число обозначается n!.
Вернемся к нашей задаче. Итак, кучеру предстояло сделать 120 перепряжек. Если он на каждую затратит только минуту времени, то на все ему понадобится 2 часа. Кучер проспорил.
