Движение любоготела в реальных условиях никогда не бывает строго равномерным и прямолинейным. Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения называют неравномерным движением.
Ускорение. При неравномерном поступательном движении скорость тела изменяется с течением времени. Процесс изменения скорости тела характеризуется ускорением. Ускорением называется векторная величина, равная отношению очень малого изменения вектора скорости D v к малому промежутку времени D t , за которое произошло это изменение:
a= D v/ D t (2.1)
Если за промежуток времени D t тело из точки А траектории переместилось в точку B и его скорость изменилась от v 1 до v 2 , то изменение скорости D v за этот промежуток времени равно разности векторов v 1 v 2 :
D v =v 2 -v 1
Направление вектора ускорения а с направлением вектора изменения скорости D v при очень малых значениях промежутка D t , за который происходит изменение скорости.
Если тело движется прямолинейно и скорость его возрастает по модулю, то направление вектора ускорения совпадает с направлением вектора скорости v 2 ; при убывании скорости по модулю направление вектора ускорения противоположно направлению вектора скорости v 2 .
При движении тела по криволинейной траектории направление вектора скорости изменяется в процессе движения, вектор ускорения а при этом может оказаться направлен под любым углом к вектору скорости v 2 .
Самый простой вид неравномерного движения — это равноускоренное движение. Равноускоренным называется движение с ускорением, постянным по модулю и направлению:
a= D v/ D t=const. ( 2.2)
Из формулы (2.1) следует, что при выражении скорости в метрх в секунду, а времени в секундах ускорение выражается в метрах на секунду в квадрате .
Скорость равноускоренного движения. При равноускоренном движении с начальной скоростью v 0 ускорение а равно
a=(v-v 0 )/t, (2.3)
где v — скорость в момент времени t . Отсюда скорость равноускоренного движения равна
v=v 0 +a*t (2.4)
Проекции скорости и ускорения. Для выполнения расчётов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме. Для нахождения проекции vx вектора скорости v на произвольную ось ОХ нужно найти алгебраическую сумму проекций векторов v 0 a*t на ту же ось:
v x =v 0x + a x *t (2.5)
График скорости.
Из уравнения (2.5) следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось ОХ равна нулю ( v 0x =0 ) , то эта прямая проходит через начало координат.
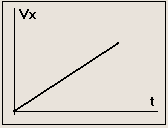
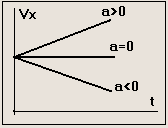
Графики зависимости проекции скорости v x от времени t для равноускоренных движений, происходящих с одинаковой начальной скоростью v 0 и различным ускорением а .
Перемещение тела при равномерном движении. Проекция s x перемещения тела за время t при равномерном движении со скоростью v определяется выражением
s x =v x t. (2.6)
Перемещение тела при равноускоренном прямолинейном движении.
Проекция s x перемещения тела за время t при равноускоренном прямолинейном движении с начальной скоростью v 0 и ускорением а определяется выражением
s x =v 0x t+(a x t 2 )/2 . (2.7)
Уравнение для координаты точки при равноускоренном движении. Для нахождения координаты x точки в любой момент времени t нужно к начальной координате x0 точки прибавить проекцию вектора перемещения на ось OX:
x=x 0 +s x (2.8)
Из выражений (2.8) и (2.7) следует:
x=x 0 +v 0x t+(a x t 2 )/2 (2.9)
