Работа по перемещению заряда в однородном поле. Сила, действующая на пробный заряд q 0 , помещенный в однородное поле E , направленное вдоль оси x , равна F = q 0 E . Работа по перемещению заряда на расстояние dx равна dA = Fdx = q 0 Edx .
Так как поле не зависит от координаты, то работа по перемещению заряда из точки x 1 в точку x 2 равна
![]() (5.1)
(5.1)
Видно, что значение работы зависит только от значений начальной и конечной координат заряда.
Всякую траекторию заряда можно представить как последовательность сколь угодно малых участков, часть которых проходится вдоль силовых линий поля (при этом совершается работа), а часть — по нормали к силовым линиям поля (на этих участках работа не совершается, так как перемещение перпендикулярно направлению силы). В результате суммирования по участкам, где заряд переносится вдоль линий поля, получается та же формуле, что и ранее. Следовательно, работа по переносу заряда в однородном поле не зависит от пути перемещения.
Работа по перемещению заряда в поле точечного заряда.
а) работа при перемещении вдоль радиуса
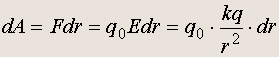
поэтому
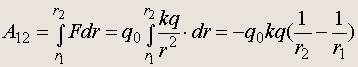 (5.2)
(5.2)
б) работа по перемещению заряда в поле точечного заряда по окружности с центром в начале координат равна нулю, так как направление силы перпендикулярно направлению перемещения;
в) при произвольном движении в поле точечного заряда траекторию можно разбить на участки, где движение происходит либо вдоль радиуса, либо по окружности. Работа по перемещению заряда из точки 1 в точку 2 дается прежней формулой.
Можно сделать вывод, что и в этом случае работа по перемещению заряда в электростатическом поле не зависит от формы пути, а зависит только от начальной и конечной точек пути.
Потенциальные поля. Если работа, совершаемая векторным полем над пробным телом, не зависит от формы траектории, то такое поле называется потенциальным . Иными словами, в потенциальном поле работа по замкнутому контуру равна нулю .
Потенциальное поле можно описать, задав значение потенциальной энергии пробного заряда в каждой точке поля и приняв по определению, что совершаемая при движении заряда работа равна взятому со знаком минус изменению потенциальной энергии W п заряда :
![]() (5.3)
(5.3)
Таким образом,
а) потенциальная энергия пробного заряда в однородном электростатическом поле:
![]()
б) потенциальная энергия пробного заряда в поле неподвижного точечного заряда:
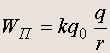
Отношение потенциальной энергии пробного заряда в электростатическом поле к величине пробного заряда зависит только от тех зарядов, которые создают поле, и называется потенциалом электростатического поля . Итак, по определению
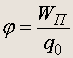 (5.4)
(5.4)
Работа по перемещению заряда из точки 1 в точку 2 запишется в виде:
![]() (5.5)
(5.5)
где величина
![]()
называется разностью потенциалов , или напряжением между точками 1 и 2.
Размерность потенциала и разности потенциалов: [ j ] = [U] = Дж/Кл = В (вольт).
Следует обратить внимание на то, что во все формулы для работы, совершаемой при движении заряда в электростатическом поле, входят не сами значения потенциальной энергии или потенциала, а разности этих значений между двумя произвольными точками. Поэтому потенциальная энергия и потенциал определены с точностью до произвольной постоянной, которую можно добавить к этим величинам, не изменив их разность между двумя точками. Это позволяет выбирать точку отсчета потенциальной энергии так, как удобно в конкретной задаче.
Связь между потенциалом и напряженностью поля. При движении заряда в однородном поле
![]()
иными словами:
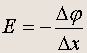 (5.6)
(5.6)
Аналогичная формула верна и в трехмерном случае. Словами это можно выразить так: электростатическое поле направлено в сторону убывания потенциала и пропорционально скорости изменения потенциала в пространстве .
Учитывая, что разность потенциалов (напряжение) U = — Dj , можно записать формулу иначе :
![]()
Полученная формула позволяет определить другую единицу измерения напряженности электрического поля: [E] = В/м (вольт на метр) .
Изменение потенциала в пространстве можно изображать, проводя эквипотенциальные поверхности (поверхности равного потенциала). Силовые линии электрического поля направлены по нормали к эквипотенциальной поверхности в каждой точке.
Потенциал заряженной проводящей сферы постоянен внутри сферы и убывает снаружи обратно пропорционально расстоянию.
