§ 3. Признаки равенства треугольников → номер 22
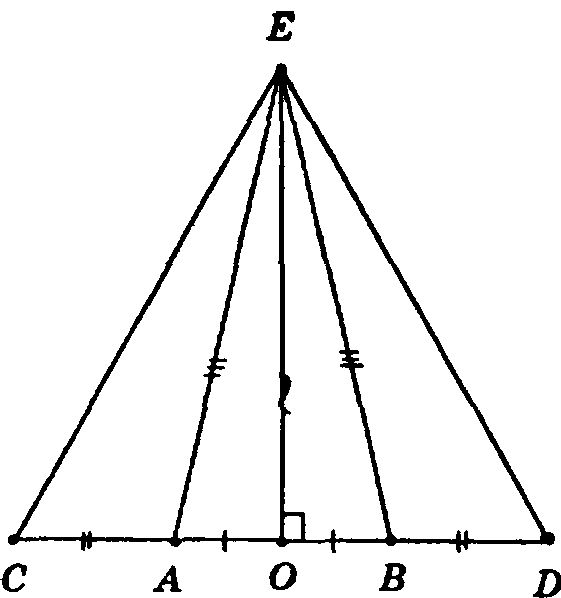
Т. к. ΔАВЕ — равнобедренный, и (∠САЕ и ∠ЕАВ), (∠ЕВА и ∠EBD) — смежные, то ∠САЕ = 180° — ∠ЕАВ = 180° — ∠ЕВА =∠EBD.
В ΔСАЕ и ΔEBD:
АЕ = ВЕ (т. к. АВЕ — равнобедренный)
∠САЕ = ∠EBD
СА = BD (т. к. СА = СО — АО = OD — OB = BD)
Таким образом, ΔСАЕ = ΔEBD, следовательно, ΔCED — равнобедренный, (т. к. СЕ = ∠ED как лежащие против равных углов в равных треугольниках), что и требовалось доказать.
