№ 23. Докажите равенство треугольников по углу, биссектрисе этого угла и стороне, прилежащей к этому углу

§ 3. Признаки равенства треугольников → номер 23

Пусть AD = A1D1 — равные биссектрисы, ∠A = ∠A1, AC = A1C1 — равные стороны.

В ΔАDС = ΔA1D1C1: ∠DAC = ∠D1A1C1 (т. к. ∠DAC половина угла ∠BAC ∠DAC = ∠BAC : 2 = ∠B1A1C1 : 2 = ∠D1A1C1).

AD = A1D1, АС = А1С1. (по условию: AD = A1D1 — равные биссектрисы, AС = A1C1 — равные прилежащие стороны).

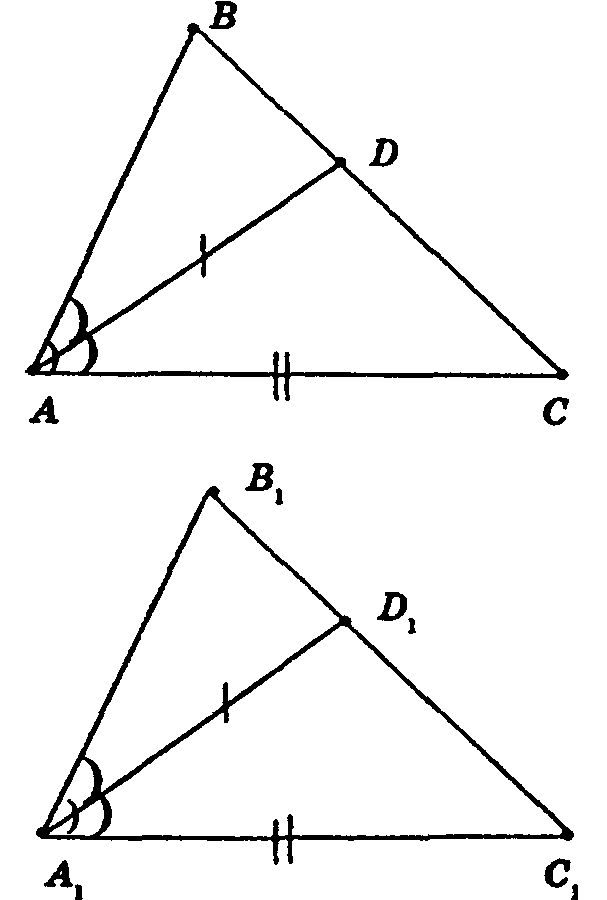
Таким образом, ΔADC = ΔА1D1C1 по 1-му признаку равенства треугольников, откуда ∠С = ∠С1 как лежащие против равных сторон в равных треугольниках)

В ΔABCи ΔА1В1С1: АС = А1С1, ∠А = ∠А1 (по условию) ∠С = ∠С1.

Таким образом, ΔABC = ΔА1В1С1 по 1-му признаку равенства треугольников, что и требовалось доказать.