§ 3. Признаки равенства треугольников → номер 35
В ΔACD и ΔBCD:
По условию: AC = CB, AD = DB, CD — общая.
Таким образом, ΔACD = ΔBCD (по 3-му признаку равенства треугольников), откуда ∠ACD = ∠BCD, ∠ADC = ∠CDB (как углы, лежащие в равных треугольниках против равных сторон). Следовательно, CD — биссектриса ∠АСВ. Аналогично доказываем, что ΔАСВ = ΔADB и ∠СВА = ∠DBA, ∠DAB = ∠CAB.
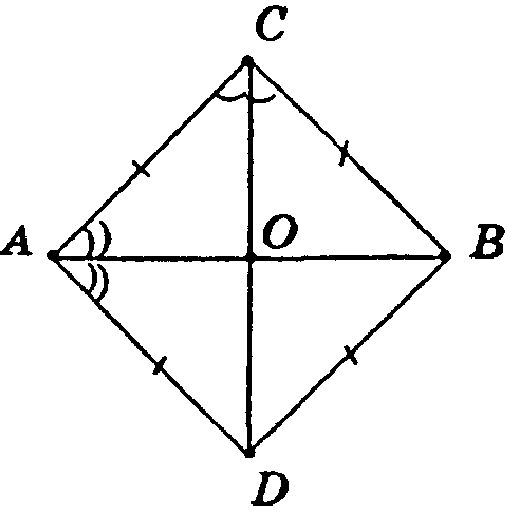
Таким образом, АВ — биссектриса ΔАСВ, что и требовалось доказать.
