Дано:
В сферическую полость радиуса поместили гантель (два одинаковых шарика массой m каждый, соединенные невесомым жестким стержнем длиной) под углом alf=pi/4 (рад) к вертикали (см. рис.1).
Найти силы давления каждого шарика на полость сразу после того, как гантель отпустили.
Радиус шариков много меньше радиуса сферы, силами трения пренебречь.
Решение
На 1-ый взгляд кажется, что сила реакции опоры для верхнего шарика (N2) равна 0. Так как сила тяжести, действующая на верхний шарик (да и на весь стержень) направлена по касательной к поверхности опоры этого шарика. Но, с одной стороны, если бы это было так, то какая бы сила придала центростремительное ускорение верхнему шарику? А это необходимо, так как с самого начала он начинает двигаться по окружности. А точнее – движение по окружности начинается именно в этой, начальной, точке. С другой стороны, как раз в этой точке ц/с ускорение равно 0 (потому что в этой точке движения (по окружности) еще нет).
Можно подумать, что центростремительная сила (а значит, и N2) и не нужна, так как вращение обеспечивает момент силы N1 относительно ЦМ (центра масс системы).
Однако анализ заставляет отказаться от этого положения. Так как показывает, что даже при элементарном перемещении (из начального положения) ЦМ смещается влево. Значит, существует какая-то сила, направленная влево. Это силой не может быть ни сила Fт, ни сила N1 (как направленные строго вертикально). Значит, сила N2 существует, и причем с самого начала не равная 0.
После этого становится понятно, в чем состоит трудность этой задачи. Она не является задачей на равновесие. Так как сразу после отпускания стержень приходит в движение (причем сразу — вращательное). С другой стороны, именно в начальный момент ц/с ускорение равно 0. То есть система является как бы частично равновесной.
Как же найти подход к такой системе?
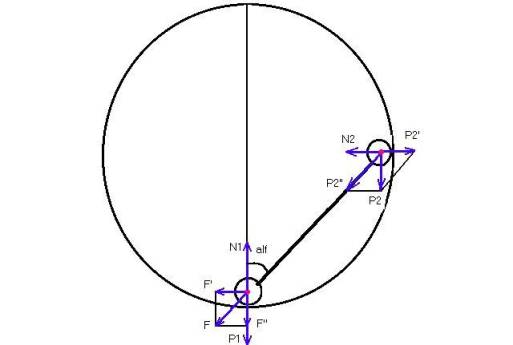
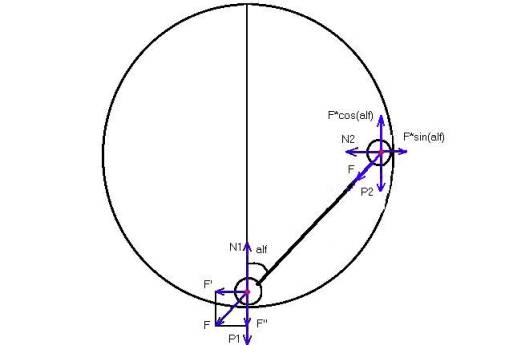
Рис.1.Силы, действующие на шарики и стержень.
Пусть верхний шарик контактирует только с поверхностью полости. Тогда сила тяжести (P2), действующая на него, не создаст силу реакции опоры, поскольку (исходя из условий задачи) направлена по касательной к этой поверхности. Но поcкольку верхний шарик контактирует также со стержнем, то он (вследствие действия на него силы тяжести) действует на стержень с силой P2” (направленной вдоль стержня), а на поверхность – силой P2’ (направленной нормально к поверхности). Такое направление этих сил имеет место потому, что природа противодействующих им сил – это упругость соответственно стержня и полости. Причем векторно (см. рис.1):
P2=P2’+P2”
Откуда алгебраически:
P2=P2”*cos(alf) => P2”=P2/cos(alf) (1a)
P2’=P2”*sin(alf) (1b)
Поскольку перемещение верх. шарика в направлении силы P2’ исключено полостью (а также отсутствует вращение шарика (около центра полости). В противном случае нужно учитывать центростремительное ускорение.), то
N2=P2’, (3)
где N2 – сила реакции опоры полости, действующая на верх. шарик.
Вследствие упругости стержня сила P2” передается через стержень на нижн. шарик:
F=P2” (4)
Эту силу заменим на 2 составляющие: касательную поверхности полости (F’) и перпендикулярную ей (F”). Отсюда:
F’=F*sin(alf); F”=F*cos(alf) (5a, 5b)
Сила тяжести (P1), действующая на нижн. шарик, поскольку она (согласно условию задачи) направлена строго перпендикулярно поверхности, создает в полном размере силу реакции опоры. Кроме этого, дополнительную силу реакции создает перпендикулярная поверхности сила F”. В итоге, поскольку перемещение нижн. шарика в направлении F” исключено полостью (а также отсутствует его вращательное движение):
N1=P1+F” (6)
Также еще из условия задачи
P1=P2=m*g (7)
Искомая величина N2 найдется из (3) после подстановки в него (1b),(1a) и (7), а величина N1 – из (6) после последовательной подстановки в него (5b),(4),(1b) и (7).
Продемонстрированный подход решает задачу также и при другом начальном расположении гантели.
***
Вроде бы, решение закончено.
Но посмотрим, чему (в итоге) равна тангенциальная составляющая равнодействующей сил, действующих на верх.шарик (R2t). Так как шарик действует на стержень с силой P2”, то стержень действует на шарик с силой той же величины, но противоположной по направлению. Поэтому (учитывая (1a)):
R2t=-P2”*cos(alf)+P2= -P2/cos(alf)*cos(alf)+P2= 0
Отсюда следует, что и тангенциальная cоставляющая ускорения верх.шарика =0. Но практически это не так! Поскольку сразу после отпускания система приходит в движение. При этом по поверхности полости скользит не только нижн.шарик, но и верхний.
Значит, сила, с которой верх.шарик действует на стержень, не равна P2” (то есть (4) неверно), а сила, с которой он действует на полость, не равна P2′ (то есть вместо (3): N2=F*sin(alf) (3а))
Рис.2.Силы, действующие на шарики и стержень (после поправки).
Отсюда:
R2t=-F*cos(alf)+P2= m*at2 (8a)
(касательная ось направлена вниз)
Соответственно для верх.шарика:
R1t=-F’=m*at1 (8b)
(касательная ось направлена влево. Что согласовано с направлением вниз)
Но как соотносятся тангенциальные ускорения шариков (at1 и at2)?
Так как шарики соединены недеформируемым стержнем, то их угловые скорости (w) одинаковы. А поскольку шарики движутся по одной траектории и сечение полости (вдоль траектории скольжения шариков) представляет из себя окружность, то шарики движутся по окружности одного радиуса — R. Значит (в каждый момент времени) равны и линейные скорости вращения шариков (т.к. v=w*R). Отсюда следует, что равны и их тангенциальные ускорения:
at1=at2=at (9)
(Заметим, что если бы шарики двигались по траекториям, отличным от окружности или по окружностям разного радиуса, то такого соотношения не было бы. То есть (9) в общем случае (для жестко связанных тел) неверно.)
Учитывая (9), из (8) найдем силу, с которой шарики действуют на стержень (F), а из уравнений (3а) и (6) – искомые силы давления шариков на полость (по 3-ему закону Ньютона равные по величине N1 и N2).