Вопрос
Помогите решить следующую задачу.
Цилиндрическая трубка радиуса r скреплена с помощью спиц с 2-мя обручами радиуса R и находится на горизонтальной поверхности. Масса обоих обручей равна M. Массой трубки и спиц можно пренебречь. На трубку намотана нить, перекинутая через невесомый блок. К концу нити прикреплен груз массы m (смотри рис.1) Обручи относительно поверхности не проскальзывают. Найти силу трения между обручами и опорной поверхностью.
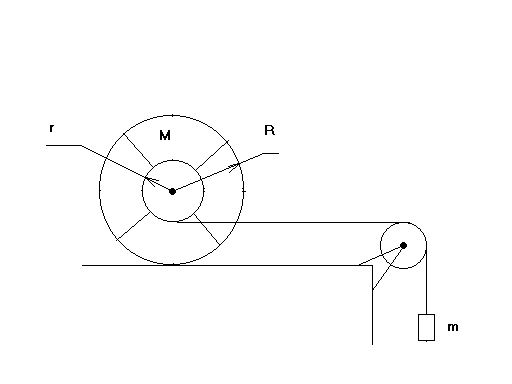
Рис.1.
Ответ
Решение задачи начнем с расстановки сил, действующих в системе (рис.2).
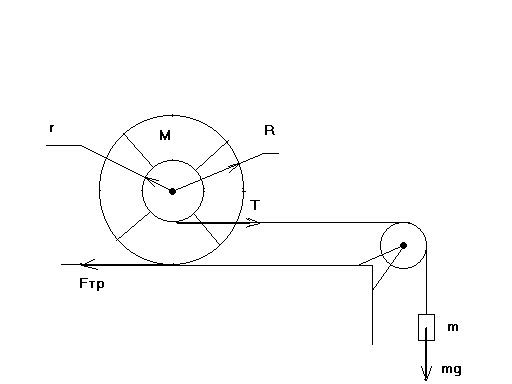
Рис.2. Силы, действующие в системе
Однако сила трения направлена влево, если обручи либо вращаются против часовой стрелки, стоя на месте, либо (без вращения) скользят по плоскости вправо. Но поскольку по условию задачи требуется отсутствие проскальзывания, то этот случай нас не интересует. В каком же случае проскальзывания не будет?
Не будем торопиться сразу писать уравнения, а порассуждаем (сначала) качественно.
Пусть обручи вращаются против часовой стрелки с угловой скоростью w, тогда линейная скорость всякой точки их обода будет v. Приведем в соприкосновение с ободом гориз. плоскость. Чтобы проскальзывание (между обручем и плоскостью) отсутствовало, плоскость должна двигаться поступательно, с линейной скоростью обода обруча v, в том же направлении (вправо)
Но есть и еще вариант: обручи, вместе с вращением, движутся поступательно относительно плоскости с той же скоростью, но в противоположном направлении. Ведь при этом относительная скорость плоскости относительно обруча будет такой же.
Таким образом, отсутствие проскальзывания возможно только тогда, когда вращение обода против часовой стрелки совмещено с его поступательным движением влево, а именно если v= -w*R, где w – угловая скорость вращения.
(Если же будет –v < w*R (обручи вращаются быстрее, чем «позволено» плоскостью (с точки зрения непроскальзывания)), то сила трения направлена влево (тормозит вращение)(или/и разгоняет поступательное движение, в правильную сторону — влево) Если же –v > w*R (обручи вращаются медленнее, чем «позволено» плоскостью (с точки зрения не проскальзывания)), то сила трения (со стороны плоскости) направлена вправо (раскручивает вращение)(или/и тормозит поступательное движение влево)
Но нетрудно понять, что соотношение скоростей v= -w*R (в данной физической ситуации) недостижимо. Поскольку сила упругости раскручивает обручи против часовой стрелки, а (поступательно) разгоняет их (согласно теореме о движении центра масс системы) вправо, а не влево.
Можно, конечно, сказать, что существует еще и сила трения, которая при определенных условиях направлена влево. Это условие — -v< w*R. Но это – недостаточное условие для того, чтобы равнодействующая сил была направлена влево. Для этого нужно, чтобы было m*g- k*(w*R+v)< 0, откуда k*(w*R+v)> m*g. Но может ли такое случиться? Определить это в рамках школьной программы невозможно.
Следовательно, каков ответ задачи?
Ответа нет.
Хотя, впрочем, а почему мы упускаем (тривиальный) случай, когда w=0 и v=0 (при t=0)? Ведь в этом случае условие v= -w*R как раз-таки выполняется! При этом Fтр=0. Это и есть ответ задачи. И скорее всего других ответов (которые мы только и пытались искать) нет.
Приложение
Точное решение задачи, посредством интегрирования системы дифференциальных уравнений
![]()
![]()
(здесь для упрощения матмодели взята линейная зависимость силы трения от относительной скорости. Это не изменяет качественного характера решения) дает следующие зависимости скорости вращения обручей и скорости поступательного движения системы от времени:
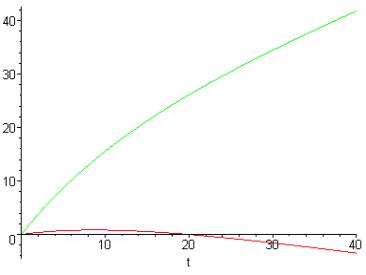
Рис.3. Зависимости скорости вращения обручей и скорости поступательного движения системы от времени (красная – w(t), зеленая – v(t))
Это показывает, что обручи сначала раскручиваются против часовой стрелки, затем останавливаются и начинают вращаться по часовой стрелке. Поступательная же скорость всегда направлена вправо. Это же показал и наш качественный анализ.
А вот как выглядит зависимость силы трения от времени:
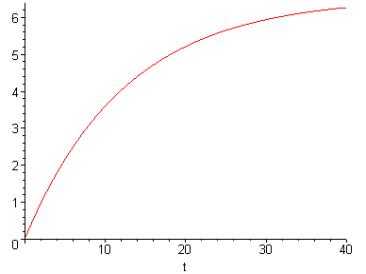
Рис.4. Зависимость силы трения от времени.
