Вопрос:
У меня не получается решить следующую задачу.
Тонкий жесткий обруч радиуса R, оставаясь в вертикальной плоскости, скатывается без проскальзывания с горки высотой h=4*R. Сила упругости, возникающая в обруче в результате его вращения, в конце спуска с горки равна T. Определите массу M обруча.
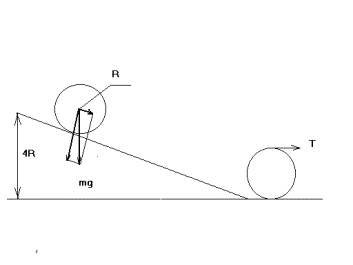
Рис.1. Условия задачи
Ответ
Решение №1
Давайте немного порассуждаем.
Сила упругости в обруче зависит от скорости вращения. Ведь центростремительное ускорение
aцс = Vвр^2/R

Рис.2. Вращение обруча
Сила упругости зависит также и от k – жесткости упругого элемента. Но с другой стороны, если k=infinity (как и дано по условиям задачи), то при любой Fупр деформация Dx=0. Значит, в этом случае Fупр определится по другой формуле. Какой?
Идея! Fупр – это именно та сила, которая сообщает частицам обруча aцс!
Поэтому
dM*Vвр^2/R= Fупр,
Где dM – это масса частицы обруча
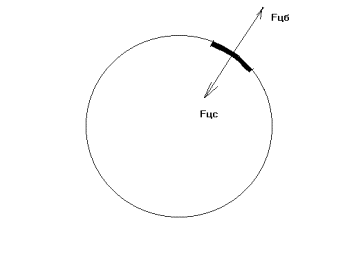
Рис.3. Силы, действующие на элемент обруча
Но какого размера частица обруча?
Или имеется в виду сила упругости, действующая на весь обруч? Но это нонсенс. Потому что на каждую частицу обруча действует своя сила упругости, а в сумме они дают 0, так как равномерно распределены и все направлены к центру.
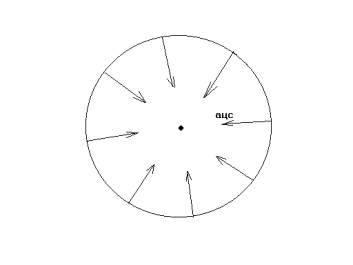
Рис.4. Распределенная сила упругости, действующая на обруч
Да, именно сила упругости, распределенная на весь обруч (то есть просуммированная по кольцу алгебраически, а не как вектор) – это то, что нужно найти в данной задаче.
Поэтому
M*Vвр^2/R= T
В этой формуле T определяется как int(dT(fi), fi=0..2*Pi). Это следует из формулы
dM(fi)*Vвр^2/R= dT(fi) (которая является уточненной версией формулы dM*Vвр^2/R= Fупр). Если её проинтегрировать по fi (угловой координате кольца) в интервале полного поворота, то есть от 0 до 2*Pi, то мы получим именно такое определение T и формулу M*Vвр^2/R= T.
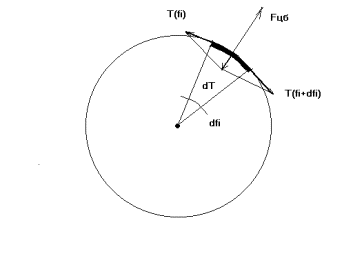
Рис.5. Как получается парциальная равнодействующая сил упругости.
Из рис.5 видно, как получается сила dT(fi) – парциальная равнодействующая парциальных сил упругости, действующих на малый элемент кольца, измеряемый угловой координатой dfi. Таких парциальных сил упругости для любого элемента кольца всегда две – T(fi) и T(fi+dfi)(как и для всякого упругого элемента). Таким образом, Т в данном случае — необычная сила.
Более того, сама задача становится разрешимой только после понимания того, о какой же силе упругости в данном случае идет речь.
Дальше решение продвигается просто.
Сначала находим Vвр. Её можно найти из закона сохранения энергии
В начале скатывания обруча его полная энергия (она складывается только из потенциальной):
E1 = M*g*h
В конце скатывания (она складывается только из кинетической):
E2 = M*Vп^2/ R = M*Vвр^2/R,
так как Vвр=Vп – проскальзывания, по условию задачи, нет.
(Иными словами, проскальзывание равно 0, так как оно и определяется как разность Vвр-Vп. Иногда говорят об относительном проскальзывании. Вполне логично это понятие определить как (Vвр- Vп)/Vвр. В более общем же случае это (V1-V2)/V1, где v1 и v2 – скорости взаимодействующих, через трение, поверхностей.)
Отсюда
Mgh = MVвр^2/2 => Vвр^2 = 2gh => T = M*2gh/R
Так как по условию задачи h=4*R, то
T = 8Mgh => M = T/(8gh),
что и требовалось найти.
Решение №2
В некоторых источниках [например, «Сборник задач по физике» под редакцией С.Н.Дмитриева, пособие для поступающих в ВУЗЫ, учебный центр МГТУ им.Баумана, М.2004] подзадача отыскания силы упругости для данной задачи решается следующим образом.
Рассмотрим дугу обруча с центральным углом alfa (рад). Масса этого элемента (в предположении постоянной плотности вдоль обруча) равна M*alfa/(2*Pi), поэтому уравнение 2-го закона Ньютона (при вращении) для него запишется в виде
M*alfa/(2*Pi)*Vвр^2/R= F (1)
где F — это равнодействующая сил упругости, с которыми действует на данный элемент (с обоих концов элемента) оставшаяся часть обруча (см. рис.5). Поскольку обруч представляет из себя последовательное соединение упругостей, то сила упругости не изменяется от сечения к сечению.
Поэтому данная равнодействующая найдется по формуле
F= 2*T*sin(alfa/2) (2)
Так как угол alfa мал, то sin(alfa/2) можно приравнять alfa/2, следовательно:
F=T*alfa (2a)
Подставляя (2a) в (1), получим уравнение для определения T, из которого:
T= M/(2*Pi)*Vвр^2/R
то есть величина T, в 2*pi раз меньшая, чем получилось в решении №1.
В чем же дело?
А вот в чем. В решении №2 считается (по традиции), что угол alfa мал. Но на самом деле он может быть любым, поэтому правильное решение относительно T получается при подстановке (2) в (1) и выглядит так:
T= M/(4*Pi)*Vвр^2/R*alfa/sin(alfa/2) (3)
Из этой формулы, в частности, выходит, что для половины обруча (то есть при alfa=pi):
T= M/4*Vвр^2/R => F=M/2*Vвр^2/R
Это же следует и из других соображений: если обруч разрезать по диаметру, то на каждую половину действует равнодействующая сил упругости, равная именно этой величине (поскольку масса каждой половины M/2)
При каком же условии допущение о малости alfa будет правомерным? Если мы будем находить равнодействующую сил упругости для бесконечно малого элемента обруча dm (соответствующего бесконечно малому углу dalfa). Уравнение 2-го закона Ньютона для него запишется так:
M*dalfa/(2*pi)*Vвр^2/R = dF = 2*T’*sin(dalfa/2)=T*dalfa
Отсюда
T’=M/(2*Pi)*Vвр^2/R = dF/dalfa
Таким образом, в решении №2 найдена не (требуемая по условию) сила упругости, а её производная по углу дуги обруча — угловое механическое «напряжение» обруча.
Чтобы найти силу упругости, нужно проинтегрировать полученную величину по центральному углу от 0 до 2*pi. Что и даст Fупр=T*2*pi= M*Vвр^2/R (см. решение №1) Именно это значение покажет динамометр, помещенный в (одинарный) разрез обруча. Поскольку в данном сечении обруч действует с силой упругости сам на себя (одним концом на другой, то есть целиком).
