Упругие одномерные соударения двух тел. Упругими соударениями тел называются соударения, при которых сохраняется кинетическая энергия. Соударения, при которых не сохраняется кинетическая энергия, называются неупругими.
В случае упругого соударения двух тел массами m 1 m 2 , скорости которых направлены по одной прямой и равны до соударения v 1н и v 2н , а после соударения — v 1к и v 2к , можно записать два закона сохранения:
![]() (17.1)
(17.1)
(сохранение импульса),
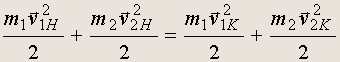 (17.2)
(17.2)
(сохранение энергии).
Из уравнений (17.1) и (17.2) получаем :
![]()
или
![]() (17.3)
(17.3)
Это означает, что относительные скорости тел до соударения и после соударения равны по величине и противоположны по знаку.
Если две частицы одинаковой массы сталкиваются, имея равные по величине и противоположно направленные скорости, то после соударения они разлетаются с равными по величине скоростями. Если одна частица догоняет другую частицу той же массы, после соударения обе частицы продолжают двигаться в ту же сторону.
Реактивное движение. Закон сохранения импульса позволяет объяснить и получить основные уравнения, описывающие реактивное движение. Главной особенностью движения ракеты является то, что это движение тела с переменной массой. Выбрасывая ежесекундно определенную часть массы в виде газов сгоревшего топлива, ракета разгоняется. Чтобы учесть переменность массы ракеты, следует воспользоваться уравнением Ньютона в форме: D p/ D t = 0 .
Здесь D p = p2 — p1 — разность конечного и начального импульсов системы, состоящей из ракеты и испущенных за время D t газов. Предполагается для простоты, что на ракету не действуют внешние силы (конечно, это не так, тяготение Земли очень важно, но в этом случае уравнения сильно усложняются). Введем обозначения : m — масса ракеты вместе с топливом, v р — скорость ракеты относительно
Земли, v г — скорость газов относительно Земли, v гр — скорость газов относительно ракеты, D mг — масса газа, вытекшего из сопла ракеты за время D t и равная уменьшению полной массы ракеты за это же время.
Начальный импульс ракеты вместе с топливом относительно Земли в произвольный момент времени равен
![]() (17.4)
(17.4)
Через время D t масса ракеты становится равной m — D mг , скорость ракеты относительно Земли получает приращение и становится равной v р + D vр . Таким образом, суммарный импульс ракеты и выброшенных газов относительно Земли равен
![]()
Принято выражать скорость газов относительно Земли через их скорость относительно ракеты (скорость истечения) v гр с помощью закона сложения скоростей: v г = v гр + v р . Это векторное равенство, и так как в большинстве случаев скорость истечения газов противоположна скорости ракеты, то |v г | < |v гр | . Подставляя это равенство в выражение для импульса системы, получаем
![]() (17.5)
(17.5)
Преобразовывая уравнения (17.4) и (17.5) получаем дифференциальное уравнение
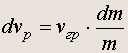 (17.6)
(17.6)
Оно носит имя нашего великого соотечественника К. Э. Циолковского. Интегрируя обе части уравнения в предположении постоянства скорости истечения газов v гр , находим закон возрастания скорости ракеты:
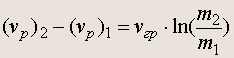 (17.7)
(17.7)
