Закон Ньютона для вращательного движения. Второй закон Ньютона для частицы, движущейся под действием силы F , может быть записан в виде:
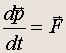
где p = mv — импульс частицы. Умножим это уравнение векторно на радиус-вектор частицы r. Тогда
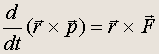(18.1)
Введем теперь новые величины — момент импульса L = r·p и момент силы N = r·F . Тогда полученное уравнение принимает вид:
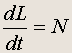
Для частицы, совершающей круговое движение в плоскости (x, y) , вектор момента импульса направлен вдоль оси z (т. е. вдоль вектора угловой скорости w ) и равен по модулю
(18.3)
Введем обозначение: I = mr 2 . Величина I называется моментом инерции материальной точки относительно оси, проходящей через начало координат. Для системы точек, вращающихся вокруг оси z с одинаковой угловой скоростью, можно обобщить определение момента инерции, взяв сумму моментов инерции всех точек относительно общей оси вращения: I = a m i r i 2 . С помощью понятия интеграла можно определить и момент инерции произвольного тела относительно оси вращения. В любом случае можно записать, что вектор момента импульса системы точек или тела, вращающихся с одинаковой угловой скоростью вокруг общей оси, равен
(18.4)
Тогда уравнение движения тела, вращающегося вокруг некоторой оси, принимает вид:
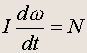(18.5)
Здесь момент силы N — вектор, направленный вдоль оси вращения и по модулю равный произведению модуля силы на расстояние по перпендикуляру от точки приложения силы до оси вращения (плечо силы).
Сохранение момента импульса в поле центральных сил. Если сила, действующая на тело со стороны другого тела (находящегося в начале координат), всегда направлена вдоль радиуса-вектора r , соединяющего эти тела, то она называется центральной силой. В этом случае векторное произведение r·F равно нулю (как векторное произведение коллинеарных векторов). Следовательно, равен нулю момент силы N и уравнение вращательного движения принимает вид dL/dt = 0 . Отсюда вытекает, что вектор L не зависит от времени. Иными словами, в поле центральных сил момент импульса сохраняется .
Утверждение, доказанное для одной частицы, можно распространить на замкнутую систему, содержащую произвольное число частиц. Таким образом, в замкнутой системе, где действуют центральные силы, сохраняется суммарный момент импульса всех частиц.
Итак, в произвольной замкнутой консервативной механической системе существуют в общем случае семь сохраняющихся величин — энергия, три компоненты импульса и три компоненты момента импульса, обладающих тем свойством, что для системы частиц значения этих величин представляют сумму значений, взятых для отдельных частиц. Иными словами, полная энергия системы равна сумме энергий отдельных частиц и т. д.
Статика. Раздел механики, изучающий условия равновесия протяженных, абсолютно твердых тел, называется статикой. Тело называется абсолютно твердым , если расстояние между любой парой его точек неизменно. По определению тело находится в состоянии статического равновесия, если все точки тела находятся в состоянии покоя в некоторой инерциальной системе отсчета.
Первое условие равновесия в ИСО: сумма всех внешних сил, приложенных к телу, равна нулю .
В этом случае равно нулю ускорение центра инерции (центра масс) тела. Всегда можно найти такую систему отсчета, в которой центр инерции покоится.
Однако это условие не означает, что все точки тела покоятся. Они могут принимать участие во вращательном движении вокруг некоторой оси. Поэтому возникает второе условие равновесия в ИСО: сумма моментов всех внешних сил относительно любой оси равна нулю .