Колебательный LC-контур.
Пусть цепь содержит только емкость C и индуктивность L . На самом деле всегда существует отличное от нуля активное сопротивление R проводов и катушки индуктивности. Однако для лучшего понимания протекающих в контуре процессов можно пренебречь активным сопротивлением и рассмотреть идеализированную модельную ситуацию.
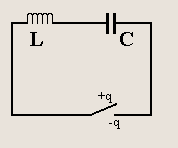
Внешний источник заряжает конденсатор, после чего отключается. В LC-контуре возникает ток из-за разрядки конденсатора. Таким образом, в произвольный момент времени в контуре имеются переменные заряд q(t) и ток I(t) .
Пусть в начальный момент времени t = 0 верхняя пластина конденсатора заряжена положительно. Ток и заряд связаны соотношением I = ± dq/dt . Выбор знака в этой формуле связан с выбором направления тока. Пусть ток направлен по часовой стрелке, тогда заряд q на пластине увеличивается, когда ток положителен, т. е. I = dq/dt .
По первому правилу Кирхгофа сумма падений напряжений на каждом элементе замкнутого контура 1-2-3-4-1 равна нулю:
Падение напряжения на индуктивности равно
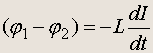
Знак в этом выражении определяется правилом Ленца: ЭДС индукции противодействует вызвавшей ее причине, т. е. если ток нарастает, dI/dt > 0 , то j2>j1 . С учетом принятого соглашения о знаках заряда на пластинах конденсатора,
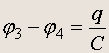
Поэтому уравнение для тока в LC-контуре принимает вид:
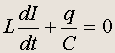
Так как I = dq/dt , то, подставляя в уравнение, получим dI/dt = d 2 q/dt 2 , так что окончательно
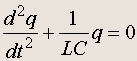(19.1)
Это уравнение описывает изменение со временем величины заряда на обкладках конденсатора.
Решение уравнения колебаний. Прямой проверкой можно убедиться, что решением уравнения для заряда в LC-контуре будет
(19.2)
где q m — максимальный заряд на пластине конденсатора, w 
— круговая частота колебаний, j — начальная фаза.
Дифференцируя выражение для q(t), можно получить выражение для тока в цепи:
Таким образом, в LC-контуре происходят гармонические колебания тока в цепи и заряда на обкладках конденсатора с частотой
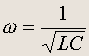(19.3)
Трансформация энергии в колебательном контуре. Полная энергия в колебательном контуре в любой момент времени складывается из энергии, запасенной в конденсаторе (электрическая энергия), и энергии магнитного поля, связанной с током в катушке индуктивности.
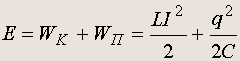
Полная энергия не меняется со временем, что проверяется прямой подстановкой значений q(t) и I(t),
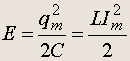(19.4)
LCR-контур. Если учесть активное сопротивление, то уравнение, вытекающее из правила Кирхгофа, примет вид:
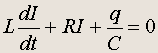
После подстановки I = dq/dt получается уравнение для изменения заряда со временем, аналогичное уравнению колебаний механической системы с учетом сил трения:
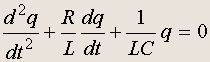
Можно убедиться, что решение этого уравнения имеет вид:
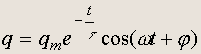(19.5)
где
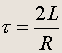
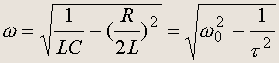
Затухание в контуре определяется соотношением параметров w 0 1/t . Если w 0 >>1/t , можно считать затухание слабым. Энергия в колебательном контуре постепенно переходит в теплоту.