§ 16. Параллельность прямых и плоскостей → номер 20
Пусть а и b — скрещивающиеся прямые, М — данная точка. Искомая прямая х вместе с каждой из этих прямых а и b определяет плоскость (аксиома 3).Пусть α и β — это плоскости.
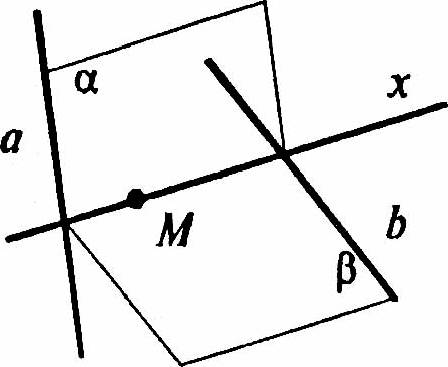
Плоскости α и β однозначно определяются точкой M и прямыми a и b (теорема 16.1). Наоборот плоскости α и β, которые мы можем построить по точке М и прямым а, b в пересечении дадут прямую х. Если прямая х пересекает прямые а и b, то х — искомая прямая. Если х будет параллельна прямым а и b, то, значит, решения не существует. Это будет если точка М принадлежит плоскости, проведенной через прямую b параллельно прямой а или же если точка М лежит в плоскости, проведенной через прямую а параллельно прямой b. Если же точка М лежит на прямой а, на прямой b, то можно провести бесконечно много прямых, удовлетворяющих условию задачи.
