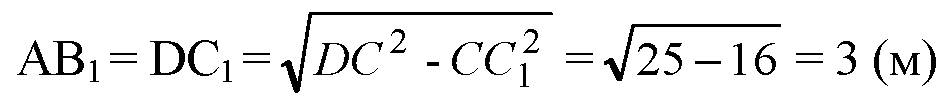§17. Перпендикулярность прямых и плоскостей → номер 28
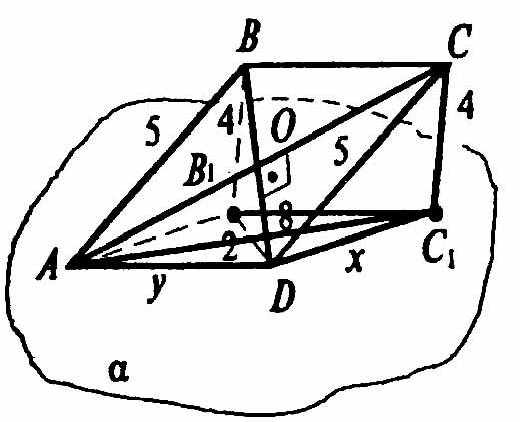
Из точек В и С опустим перпендикуляры ВВ1 и СС1 на плоскость α; ВВ1 = СС1 = 4м. АС1 — проекция диагонали АС на плоскость α, В1D — проекция диагонали BD на плоскость α. Так что АС1 = 8 м, В1D = 2 м.
Рассмотрим прямоугольные треугольники ВВ1D и СС1А. По теореме Пифагора:
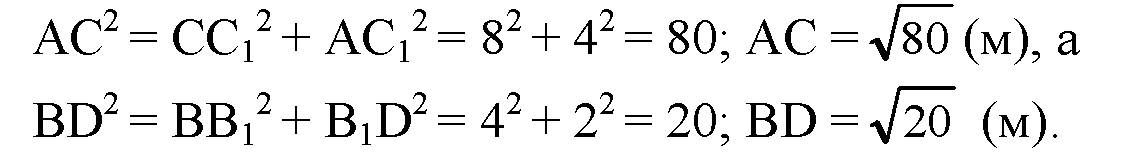
Далее
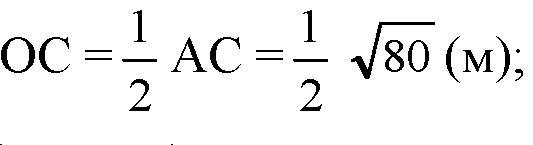
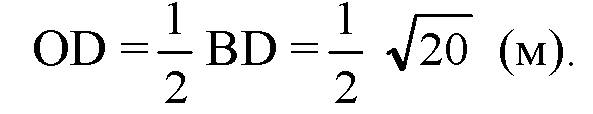
По свойству ромба: АС ⊥ BD. Так что треугольник OCD — прямоугольный, поэтому:
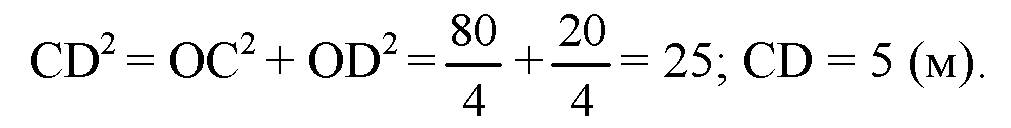
Так как ВС || α, то В1С1 = ВС = 5 (м).
Из прямоугольных треугольников DC1C и АВ1В найдем АВ1 и DC1
По теореме Пифагора: