§17. Перпендикулярность прямых и плоскостей → номер 30
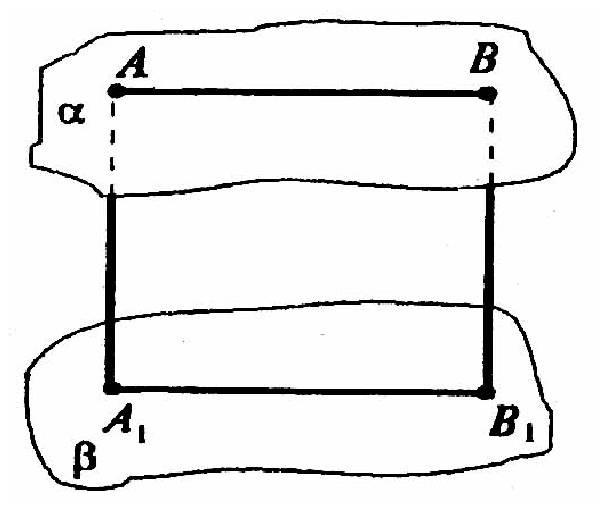
Выберем произвольные точки А и В на плоскости α, параллельной плоскости β.
Прямая АВ лежит в плоскости α поэтому параллельна плоскости β. Опустим перпендикуляры АА1 и ВВ1 на плоскость β. По теореме 18.4 прямые АА1 и ВВ1 параллельны и лежат в одной плоскости; у четырехугольника АА1В1В противоположные стороны параллельны, значит, это параллелограмм; так что, АА1 = ВВ1. Что и требовалось доказать.
