§18. Декартовы координаты и векторы в пространстве → номер 28
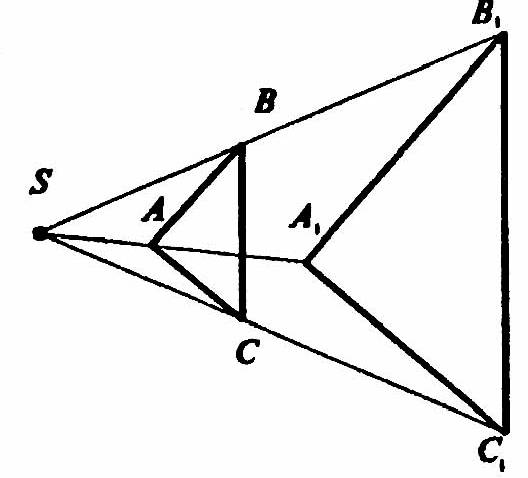
Пусть S — центр гомотетии, тогда
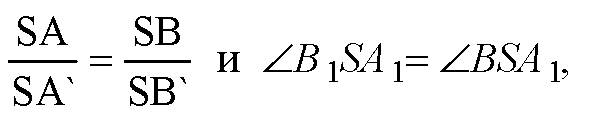
Так что ΔSAB~ΔSA1В1, значит
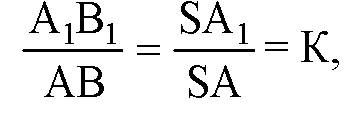
Аналогично,
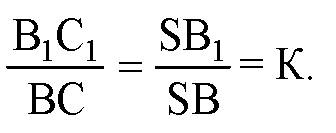
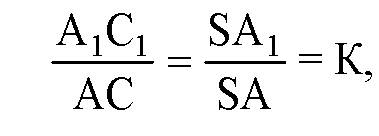
Где К — коэффициент гомотетии.
Следовательно,
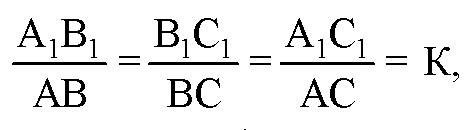
И по третьему признаку ΔАВС ~А1В1С1, то есть преобразование гомотетии в пространстве является преобразованием подобия. Что и требовалось доказать.
