29. Три прямые, проходящие через точку S, пересекают данную плоскость в точках А, В, С, а параллельную ей плоскость в точках А1, В1, С1. Докажите, что треугольники АВС и А1В1С1 гомотетичны

§18. Декартовы координаты и векторы в пространстве → номер 29

Имеем AB || A1B1; AC || A1C1; BC || B1C1, т. к. эти прямые лежат в плоскостях SA1B1, SA1C1, SB1C1 соответственно, и в параллельных плоскостях α и β. Так что ∠SAC = ∠SA1C1, ∠SCA = &nag;SC1A1, как соответственные.

И значит, ΔSAC ~ ΔSA1C1 (по двум углам). Аналогично, ΔSAB ~ ΔSA1B1, ΔSBC ~ ΔSB1C1.

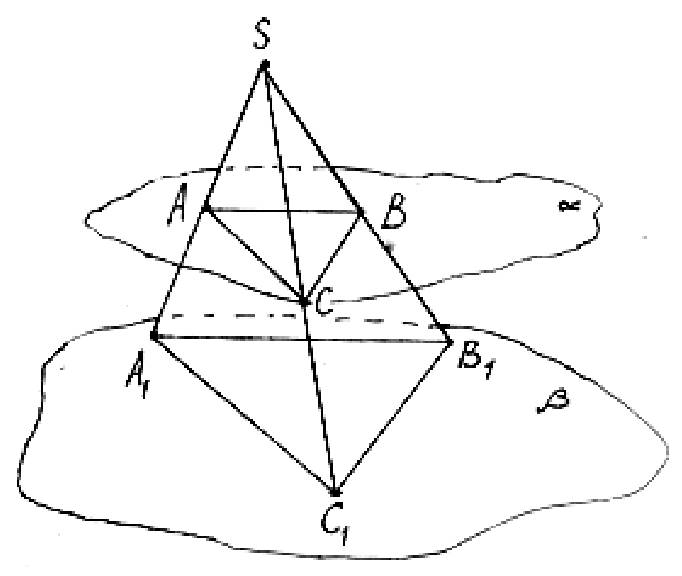
Из подобия треугольников следует:

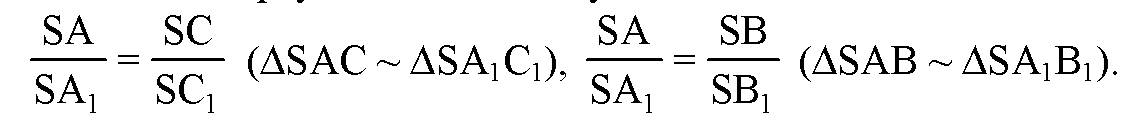
Так что

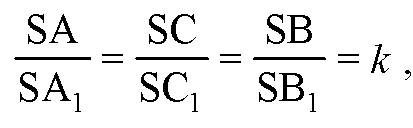
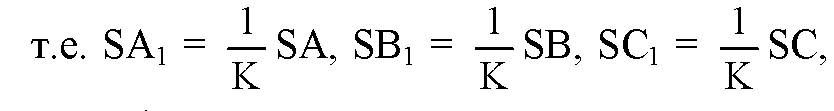
Где К — коэффициент подобия.

А, значит, ΔABC и ΔA1B1C1 гомотетичны. Что и требовалось доказать.