34. Точка А лежит вне плоскости α, Х — произвольная точка плоскости α, Х1 точка отрезка АХ, делящая его в отношении m : n. Докажите, что геометрическое место точек Х1 есть плоскость, по параллельная плоскости α

§ 16. Параллельность прямых и плоскостей → номер 34

Возьмем в плоскости α произвольную точку Х, построим соответствующую точку Х1 (АХ1 : ХХ1 = m : n) и проведем через точку Х1 плоскость β, по параллельную α. Докажем, что плоскость β — соответствующее геометрическое место точек.

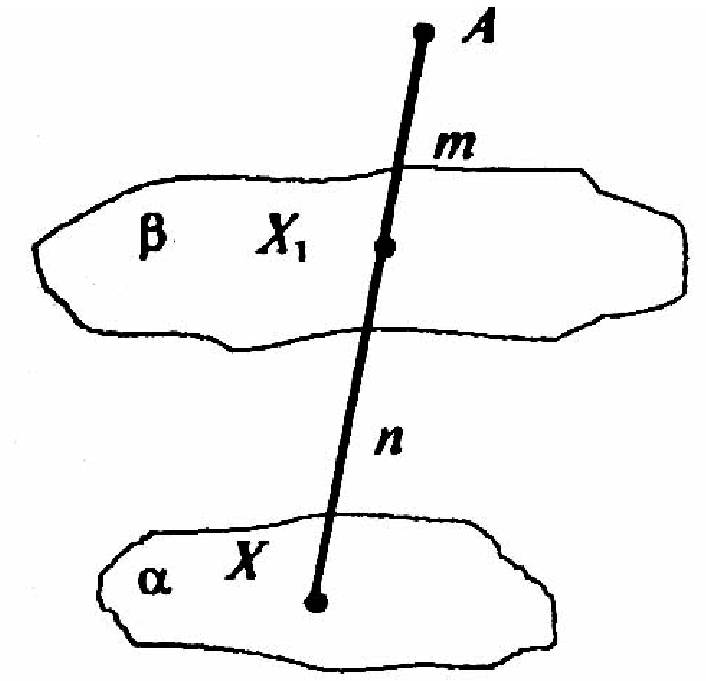
1) Для любой точки Y плоскости α точка Y1 пересечения прямой АY1 : Y1Y = АХ1 : Х1Х = m : n, отсюда следует, что любая точка плоскости β удовлетворяет данному условию.

2) Если для точки Y плоскости α точка Y2 делит отрезок АY в отношении m : n, то из соотношения пункта 1 следует, что точка Y2 совпадает с точкой Y1 и поэтому принадлежит плоскости β.

Два указанных утверждения означают, что рассматриваемое геометрическое место точек есть параллельная плоскости α плоскость в.