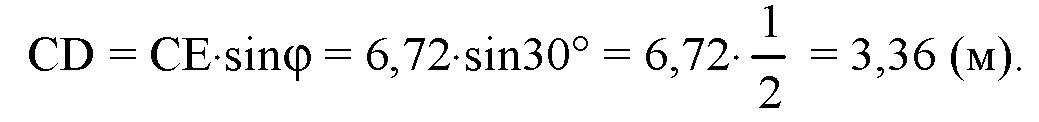§18. Декартовы координаты и векторы в пространстве → номер 47
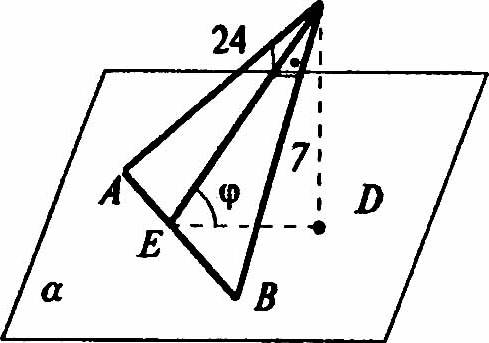
Пусть АСВ — данный треугольник. Проведем CD ⊥ а, где плоскость α проходит через гипотенузу АВ и образует ∠φ = 30°. Проведем СЕ ⊥ АВ. Тогда ∠CED = ∠φ = 30°.
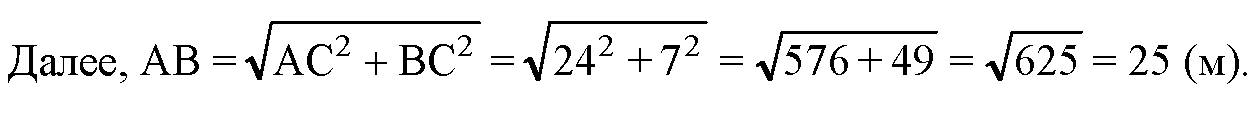
Далее,
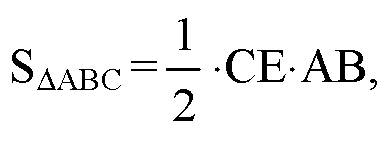
, с другой стороны:
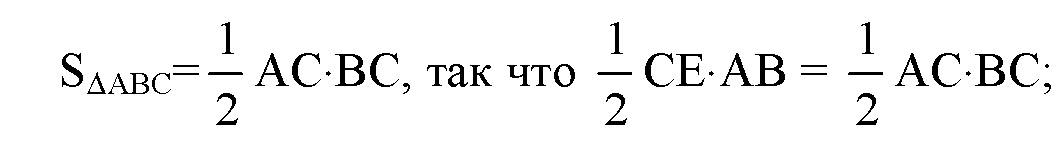
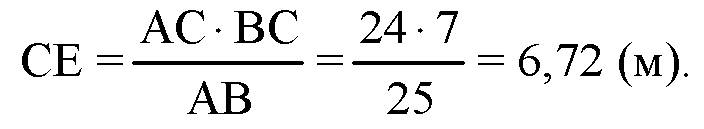
Из ΔCDE найдем искомое расстояние: