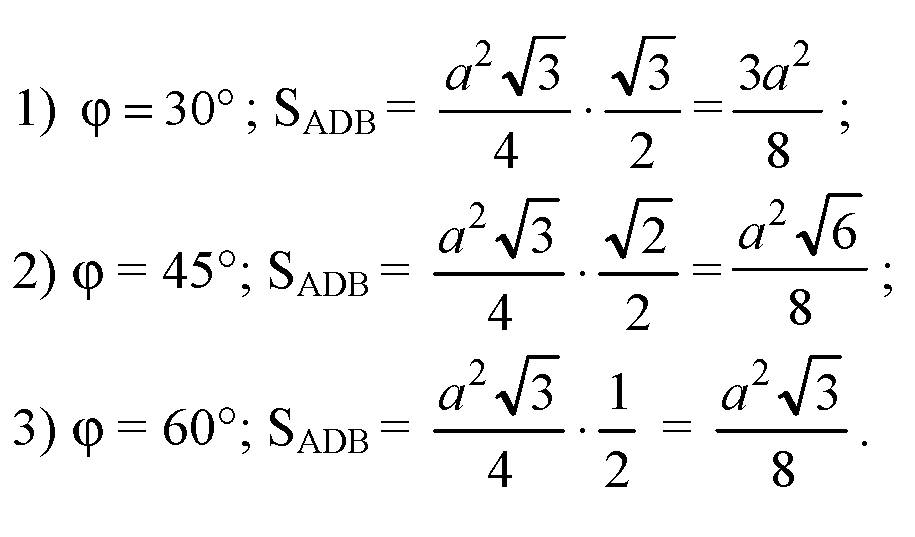§18. Декартовы координаты и векторы в пространстве → номер 48
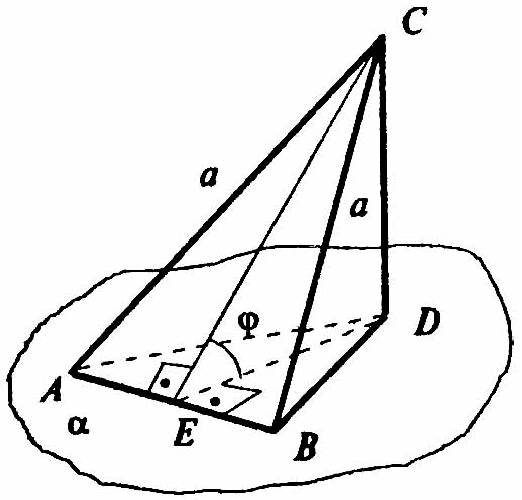
Пусть ΔABC — данный, равносторонний. Проведем высоту СЕ, и CD — перпендикуляр к плоскости α. Тогда по теореме о трех перпендикулярах ее проекция ED будет высотой треугольника ADB, угол CED — угол между плоскостями ACD и α, т. е. ∠CED = φ.
Из прямоугольного треугольника CED: ED = СЕ•cosφ. ADB — ортогональная проекция треугольника АСВ на плоскость α. Тогда

Так как ΔABC — равносторонний.
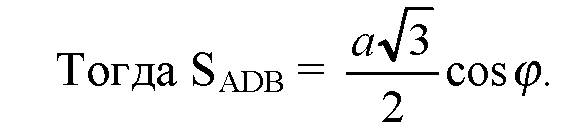
Так что: