Дополнительные задачи к главе I Параллельность прямых и плоскостей. → номер 101
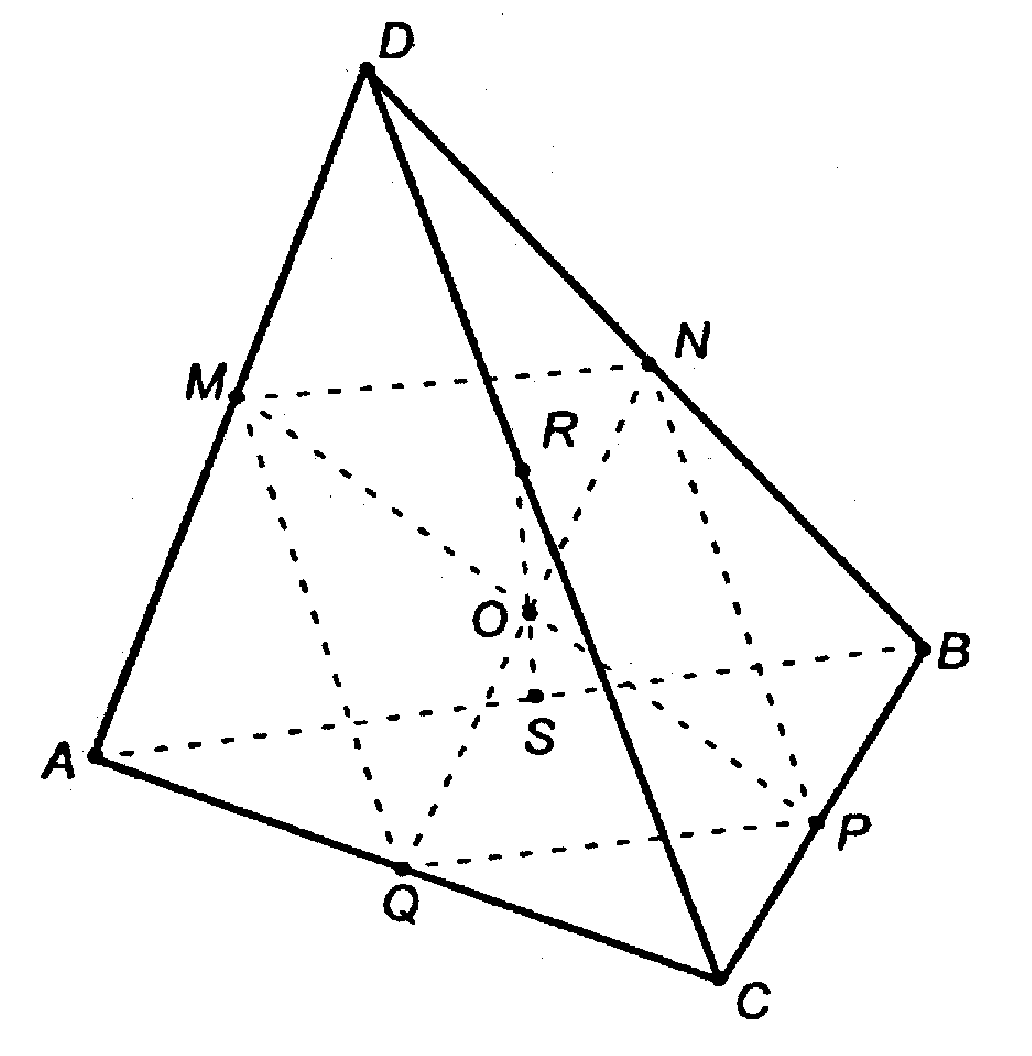
Соединим середины ребер, лежащих в одной грани; получим, что каждый из отрезков будет средней линией соответствующего треугольника.
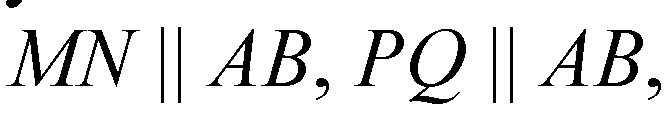
Поэтому
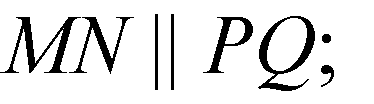
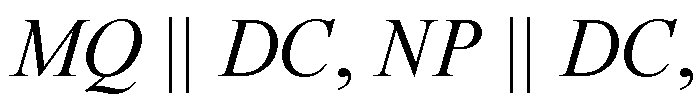
Поэтому
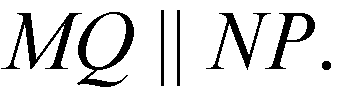
Значит, 4-угольник MNPQ — параллелограмм по определению, его диагонали QN и МР пересекаются в т. О и делятся в ней пополам. Отрезки QN и MP соединяют середины противоположных ребер тетраэдра.
Повторяя проведенные выше рассуждения, заключаем, что RS и QN тоже пересекаются в точке О и делятся ей пополам.
Таким образом, все три отрезка: RS, QN, MP — пересекаются в т. О и делятся в ней пополам.
Утверждение доказано.
